Versicherungsfachmann (Aktuar) Wolfgang Abele hat sich die Studie der Versicherungsforen Leipzig näher angesehen und zeigt fundamentale Schwächen auf.
Im Jahr 2011, auf dem Höhepunkt der deutschen Anti-AKW-Hysterie kurz nach Fukushima, veröffentlichte die Versicherungsforen Leipzig GmbH eine im Auftrag des Bundesverbands Erneuerbare Energien erstellte Studie mit dem Titel »Berechnung einer risikoadäquaten Versicherungsprämie zur Deckung der Haftpflichtrisiken, die aus dem Betrieb von Kernkraftwerken resultieren«. Diese Studie wurde damals sogar im Spiegel und im Manager-Magazin wohlwollend besprochen. Seitdem wird sie gern zitiert, um zu beweisen, dass Kernkraftwerke nicht versicherbar seien. In diesem Sinne erklärte im Januar 2022 auch Matthias Land aus dem Ausschuss Schadenversicherung der Deutschen Aktuarvereinigung (DAV) im Versicherungsmagazin, die Studienergebnisse seien valide, und deshalb sehe die DAV die Kernkraft als nicht nachhaltig an.
In der Studie wird der maximale Schaden durch einen nuklearen Katastrophenfall (»Super-GAU«) in Deutschland mit 6,09 Billionen Euro beziffert. Die Eintrittswahrscheinlichkeit betrage 1:1000 pro Reaktorbetriebsjahr. Daraus wird eine Jahresprämie pro Kernkraftwerk von 19,6 Milliarden Euro abgeleitet.
Kernkraftwerke sind versichert
Zum Hintergrund: Alle deutschen Kernkraftwerke sind beziehungsweise waren versichert. Die Prämie lag zuletzt im unteren zweistelligen Millionenbereich, die Deckung bei zirka 2,5 Milliarden Euro. Das ist im internationalen Vergleich hoch. In Deutschland, der Schweiz, Japan und vielen weiteren Ländern gilt darüber hinaus eine unbegrenzte Haftung des Betreibers.
Da die Betreiber jedoch weder einen Schaden von 6,09 Billionen Euro noch eine jährliche Versicherungsprämie von 19,6 Milliarden Euro pro Kernkraftwerk bezahlen können, entstünde daraus für die Allgemeinheit ein untragbares finanzielles Risiko. Würde man diese externen Kosten auf den Strompreis umlegen, wäre er um ein Vielfaches höher, so die Studie.
In diesem Artikel schauen wir uns die Vorgehensweise und Zahlenbasis im Detail an. Dies lässt Rückschlüsse auf Qualität und Aussagekraft der Studie zu.
Vorgehensweise
Die Studie, nachfolgend als VL bezeichnet, stellt keine eigenen Schätzungen an, sondern wählt Ergebnisse aus anderen Studien aus und kombiniert und gewichtet diese. Die wichtigsten Quellen sind Arbeiten deutscher Ökonomen, die bereits zirka 20 Jahre früher veröffentlicht wurden. Es werden unter anderem die Kosten tödlicher und nicht tödlicher Krebserkrankungen sowie genetischer Schäden nach einem Super-GAU geschätzt. Mit Abstand die teuerste Schadensart sind tödliche Krebserkrankungen. Ihre Anzahl wird in VL berechnet durch diese Formel
Anzahl Krebstodesfälle = kollektive Strahlendosis × Risikokoeffizient
Linear-No-Threshold-Modell als Berechnungsbasis
Die Basis dieser simplen Berechnung ist das Linear-No-Threshold-Modell (LNT). Nach diesem Modell besteht zwischen Strahlendosis und Krebsrisiko ein linearer Zusammenhang. Also: eine doppelte Dosis führt zu einem doppelt so hohen Krebsrisiko, die halbe Dosis führt zu einem halb so hohen Krebsrisiko. Dies soll nach dem LNT-Modell auch für sehr kleine Dosen gelten.
Beispielsweise enthalten Bananen nennenswerte Mengen an radioaktivem Kalium-40. Wer eine Banane isst, erhält dadurch eine Strahlendosis von 0,0000001 Sievert. Die Kollektivdosis, die für VL in der oben genannten Formel eine wichtige Rolle spielt, ist die Summe der Einzeldosen für eine gegebene Bevölkerungsgruppe. Essen beispielsweise 10 Millionen Personen im Laufe eines Jahres je 20 Bananen, beträgt die Kollektivdosis 20 Sievert. Bei einem Risikokoeffizient von 5 % pro Sievert ist nach der VL-Formel bereits ein Krebstoter durch den Verzehr von Bananen zu erwarten. Nicht alle finden das plausibel.
Kollektivdosis untauglich zur Prognose von Krebstodesfällen
Die Strahlenschutzbehörden halten dennoch an LNT fest. Sie differenzieren jedoch je nach Anwendungszweck. Ausdrücklich nicht zu den sinnvollen Anwendungen zählt laut Internationaler Strahlenschutzkommission (ICRP) die Prognose von Krebstodesfällen auf Basis der Kollektivdosis (Hervorhebungen durch den Autor):
»Die „kollektive effektive Dosis” ist eine Größe, die für die Optimierung verwendet wird, d.h. für den Vergleich radiologischer Technologien und für Verfahren des Strahlenschutzes, in erster Linie im Zusammenhang mit beruflicher Exposition. Die kollektive effektive Dosis ist nicht als Größe für epidemiologische Risikoabschätzungen gedacht, und sie ist ungeeignet für die Verwendung bei Risikovorhersagen. Die Summierung sehr niedriger individueller Dosen über ausgedehnte Zeiträume ist nicht sinnvoll. Dies gilt insbesondere für die Berechnung von Krebstodesfällen.«
Die VL-Autoren erwähnen diese Warnungen zwar, setzen sich jedoch darüber hinweg. Sie berufen sich auf ihre Hauptquellen, die 20 Jahre früher veröffentlicht wurden: »Neuere und genauere Studien zur Unfallfolgenabschätzung in Kernkraftwerken in Deutschland liegen nicht vor« (VL, S. 43).
Studie der Versicherungsforen Leipzig basiert auf ungültigen Verfahren
Noch einmal: Was die Fachwelt ablehnt, findet VL legitim. Man hat keine validen Quellen, also nimmt man welche, die auf einem ungültigen Verfahren basieren. Gemäß dieses ungültigen Verfahrens rechnet VL wie folgt:
Krebstodesfälle = Kollektivdosis × Risikokoeffizient × Faktor Bevölkerungsdichte
Der zusätzliche »Faktor Bevölkerungsdichte« wird benötigt, weil man die Tschernobyl-Dosis auf Deutschland umrechnen will.
VL berücksichtigt vier verschiedene Schätzungen für die Kollektivdosis und fünf verschiedene Schätzungen für die Bewertung der Todesfälle. Daraus ergeben sich 20 verschiedene Schadensummen (VL, S. 60):
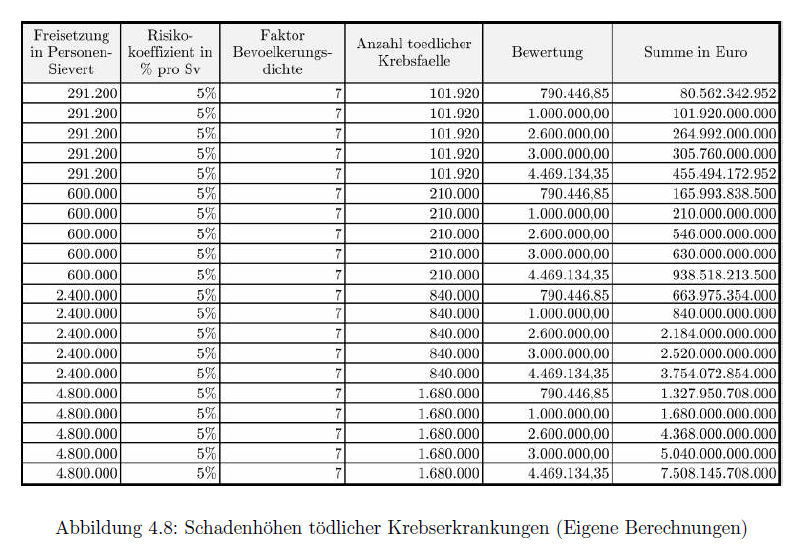
Freisetzung in Personen-Sievert
Die in Spalte 1 der obigen Tabelle geschätzten kollektiven effektiven Dosen, die in Tschernobyl freigesetzt wurden, stammen aus folgenden Quellen:
| 291.200 | EU-Bericht Externe Kosten der Atomenergie 1995. Von einem französischen Institut berechnet. Anders als in VL dargestellt, ist diese Zahl eine Schätzung für einen “major reactor accident” in einer “central region of western Europe”, nicht für Tschernobyl. “The Chernobyl accident is not considered to be in any way representative of what would happen in reactors built and operated in western countries.” Die Frage, ob sich Tschernobyl angesichts der unterschiedlichen Reaktortypen und Sicherheitsstandards überhaupt auf Deutschland übertragen lässt, wird in VL nicht gestellt. |
| 600.000 | The Other Report on Chernobyl (TORCH). Von den europäischen Grünen beauftragt. Stimmt überein mit der ersten Schätzung von UNSCEAR 1988. In UNSCEAR 2008 wurde die Schätzung um ca. 30 % reduziert. (UNSCEAR: United Nation Scientific Committee on the Effects of Atomic Radiation, wissenschaftlicher Ausschuss der Vereinten Nationen zur Bewertung der Auswirkungen ionisierender Strahlung). |
| 2.400.000 | Hohmeyer 1989. Nicht verifizierbar. Hohmeyer will die Zahl dem allerersten Bericht entnommen haben, den sowjetische Wissenschaftler vier Monate nach Tschernobyl 1986 für die International Atomic Energy Agency IAEA erstellten. Die IAEA folgte in ihren späteren Berichten hingegen der UNSCEAR. |
| 4.800.000 | Ewers/Renning 1992. Hohmeyer mal 2. Warum Ewers/Renning lieber Hohmeyer mal 2 nahmen statt UNSCEAR 1988, ist unklar. |
Faktor Bevölkerungsdichte
Den Faktor Bevölkerungsdichte setzt VL mit 7 an. VL übernimmt ihn von Ewers/Renning, die ihn mit einer siebenfach höheren Bevölkerungsdichte in Deutschland begründen.
VL wendet diesen Faktor allerdings auf zwei der vier Schätzungen der Kollektivdosis falsch an:
- In der Schätzung von 291.200 Personen-Sievert ist die kollektive Dosis bereits auf westeuropäische Verhältnisse skaliert. Entsprechend nennt ExternE statt 101.920 nur 11.575 als Anzahl tödlicher Krebsfälle (S. 202–204).
- Inkorrekt ist auch die Anwendung auf die Schätzung mit 600.000 Personen-Sievert, da damit die weltweite Belastung gemeint ist. UNSCEAR 2008: “The total collective effective dose equivalent commitment from the accident is estimated to be 600,000 man Sv. From Table 24, it is seen that 53% is experienced in European countries, 36% in the USSR, 8% in Asia, 2% in Africa and 0.3% in North, Central and South America.” Auf Deutschland entfiele also nur ein Bruchteil davon.
Risikokoeffizient
Der Risikokoeffizient von 5 % pro Sievert stammt aus einer ICRP-Publikation von 1990. Er sollte nur maßnahmentechnisch angewendet werden, siehe oben.
Bewertung Todesfall
Wie ist ein Todesfall zu bewerten? Wir gehen hier nicht auf die verschiedenen Ansätze ein, sondern verweisen nur darauf, dass der höchste Wert 4,469 Mio. Euro pro Person wieder von Ewers/Renning stammt.
Maximalschaden
Offensichtlich ist die Spannweite der Schadensummen von 80 Milliarden bis 7,5 Billionen Euro in der Tabelle riesig, und ohne den inkorrekten Faktor 7 in der ersten Schätzung wäre sie sogar noch größer. Wie soll man diese höchst unterschiedlichen Expertenschätzungen bewerten? Welche sind plausibel? Welche eher nicht?
Als Bewertungskriterien kommen Gründlichkeit, Aktualität, Neutralität etc. in Betracht. Man könnte beispielsweise die wissenschaftliche Herleitung der Strahlendosis mit genauen Unterscheidungen nach Personengruppen und Regionen in UNSCEAR 2008 mit der Daumenschätzung in Ewers/Renning vergleichen. Es erscheint auch plausibel, dass unmittelbar nach der Jahrhundertkatastrophe von Tschernobyl noch nicht alle Informationen vorlagen. Deshalb dürften spätere Forschungsarbeiten verlässlicher sein. Schließlich könnte man die offiziellen Untersuchungsberichte einer UN- oder EU-Behörde als glaubwürdiger einstufen als etwa Berichte im Auftrag eines Lobbyverbands oder einer Nichtregierungsorganisation.
Keine inhaltliche Differenzierung
Auf eine solche inhaltliche Bewertung verzichtet VL jedoch. Stattdessen berechnet VL als maximalen Schaden eine Summe, die sich aus der Hälfte der zahlenmäßig höchsten Einzelschätzung und der Hälfte des Mittelwerts aller anderen Schätzwerte ergibt. VL erläutert dies auf S. 91 wie folgt:
»Für die Schadenart tödliche Krebserkrankungen liegen beispielsweise 20 Schadenhöhen vor. Der höchste Wert geht mit 50 Prozent in die Schadensummenermittlung ein. Die verbleibenden 50 Prozent werden gleichmäßig unter den restlichen 19 Werten aufgeteilt. Die Berechnung erfolgt somit nach folgender Vorgehensweise:
Durch diese Gewichtung garantiert VL, dass das Endergebnis immer in der Größenordnung der höchsten Schätzung (> 50%) liegt, ganz egal, wie qualitativ gut oder schlecht diese Schätzung hinsichtlich der oben genannten Bewertungskriterien ist. Alle moderaten Schätzungen fallen unter den Tisch.
Da Ewers/Renning 1992 in allen Kategorien (Personen-Sievert, Krebsfälle, Bewertung) ganz weit oben rangieren und (inflationiert für 2011) 8,3 Billionen Euro als Maximalschaden ermitteln, ist es wenig überraschend, dass VL mit 6,09 Billionen Euro auf einen Wert in derselben Größenordnung kommt.
Anstieg des Meeresspiegels nach VL-Methode
Nehmen wir an, wir wollten mit der VL-Methode den maximalen Anstieg des Meeresspiegels bis zum Jahr 2100 durch den Klimawandel schätzen. Dazu betrachten wir drei unterschiedliche Schätzungen: Es gibt die Schätzung des Weltklimarats im 6. Sachstandsbericht von 2021, der eine Erhöhung um 0,44 m vorhersagt, eine alternative Schätzung, die 2 m prognostiziert, und es gibt den Maya-Kalender, der anhand von Himmelsbeobachtungen die Sintflut vorhersagt, sagen wir, 100 m. Die VL-Methode nimmt den höchsten Wert, also die 100 m der Maya, bildet davon 50 %, also 50 m, und addiert den Mittelwert 1,22 m der übrigen Schätzungen. Insgesamt ergibt sich ein erwarteter Anstieg des Meeresspiegels um 51,22 m. Ob aber die Methode der Maya überhaupt prinzipiell zu brauchbaren Prognosen führen kann, wird gar nicht hinterfragt.
Kritik an Studie vom Forum Ökologisch-Soziale Marktwirtschaft
Dass diese Zahlen mehr als nur ein klein wenig überzogen sein könnten, bemerkte 2012 sogar das nicht unbedingt als kernkraftfreundlich bekannte Forum Ökologisch-Soziale Marktwirtschaft:
»Aus heutiger Sicht ist die Schätzung der Schadenskosten eines Super-GAU von Ewers/Rennings 1992 keine geeignete Grundlage, weil dort auch im Vergleich zu aktuelleren Studien eine sehr hohe Anzahl von Krebstoten, ein hoher Wertansatz für Todesfälle (6 Mio. DM 1989, entspricht 4,8 Mio. € 2012) sowie eine hohe Eintrittswahrscheinlichkeit angenommen wurde, die die Option von Accident-Management-Maßnahmen nicht berücksichtigt.« (Externe Kosten der Atomenergie und Reformvorschläge zum Atomhaftungsrecht, Studie im Auftrag des Bundesverbands Windenergie und Greenpeace Energy 2012)
Anzahl Krebstoter aus heutiger Sicht
Wie bereits erwähnt, führt VL keine Betrachtung durch, wie plausibel die jeweiligen Projektionen sind. UNSCEAR 2008 wird nicht einmal erwähnt. Wie plausibel sind also 1,68 Millionen Krebstote aus heutiger Sicht? Dazu sagte die Leiterin der Chernobyl Tissue Bank, Geraldine Thomas, 2020 in einem Interview:
»Schilddrüsenkrebs ist glücklicherweise eine der am besten behandelbaren Krebsarten überhaupt: Von hundert betroffenen Patienten stirbt einer innerhalb von 50 Jahren. Da wir erstens die Strahlendosen der Bewohner aus den Risikogebieten kennen und zweitens die Zahl der betroffenen Bewohner, können wir sagen: Es gibt wahrscheinlich 16.000 Fälle von strahleninduziertem Schilddrüsenkrebs. Das heißt, dass etwa 160 Menschen daran verstorben sind oder noch sterben werden.«
Andere Krebsarten wurden nur marginal registriert. Multipliziert man die von Thomas genannte Zahl 160 mit dem Faktor 7 aufgrund der höheren Bevölkerungsdichte, kommt man auf 1.120 Fälle. Das sind genau 1500-mal weniger als die 1,68 Mio. in VL.
Vergleich mit anderen Energieformen fehlt
VL betrachtet auch nicht die realen Daten zu tödlichen Unglücksfällen in der Energiewirtschaft. Gemessen an Todesfällen pro Terawattstunde sind Kernkraftwerke, inklusive Tschernobyl und Fukushima, eine der sichersten Stromerzeuger überhaupt, etwa gleichauf mit den Erneuerbaren.
Eintrittswahrscheinlichkeit
Wodurch kann es überhaupt zu einem Super-GAU mit radioaktiven Freisetzungen kommen? Wie wahrscheinlich ist das? In VL ist Terror der wichtigste Auslöser, er überragt bei der Eintrittswahrscheinlichkeit alle anderen Risiken. Als Eintrittswahrscheinlichkeit wird 1:1.000 pro Reaktorjahr angegeben. Eine Begründung für diese Wahrscheinlichkeit nennt VL nicht.
Zum Vergleich: Bei Ewers/Renning ist die Wahrscheinlichkeit 1:33.000. Und die findet selbst das Forum Ökologisch-Soziale Marktwirtschaft zu hoch, da darin keine Notfallmaßnahmen berücksichtigt seien. Ob Flugzeugabstürze oder Beschuss durch Panzerabwehrwaffen einen Super-GAU auslösen können, noch dazu einen mit radioaktiven Freisetzungen, ist ebenfalls fraglich, wenn man die Seiten der World Nuclear Association zum Thema Reaktorsicherheit liest. Dass Terror seit dem 11. September 2001 üblicherweise in Versicherungen ausgeschlossen wird und daher keinen Einfluss auf die Versicherungsprämien hat, erwähnt VL auch nicht.
Robert Wilson hat vorgerechnet, was eine Eintrittswahrscheinlichkeit von 1:1.000 pro Reaktorjahr bei insgesamt ca. 440 Kernkraftwerken weltweit bedeutet. Es müsste im Mittel fast jedes zweite Jahr einen Terrorangriff auf ein Kernkraftwerk geben. Die Wahrscheinlichkeit für mindestens einen Anschlag in 20 Jahren liegt bei
1 – (1 – 1/1000)440*20 = 99,985 %
Es hätte demnach mit an Sicherheit grenzender Wahrscheinlichkeit einen Anschlag geben müssen. Tatsächlich gab es keinen einzigen.
Statistik
Die Versicherungsprämie wird in VL genauso berechnet wie in der Kfz-Versicherung. Sie ergibt sich aus dem erwarteten Schaden im Deckungszeitraum plus einem Risikozuschlag. Dieser wiederum besteht aus einem Faktor multipliziert mit der Standardabweichung. Der Faktor ist oft 3, im Prinzip aber Ermessenssache. Von Kosten, Provisionen und Gewinnmarge wird in VL abgesehen. Da der erwartete Schaden mit 5,8 Billionen Euro bereits feststeht, könnte man direkt zur Bestimmung der Jahresprämie gehen. Stattdessen bemüht VL zuerst in den Kapiteln 6.1. bis 6.2.2 einen aufwendigen statistischen Apparat, der am Ergebnis fast nichts ändert. Vorher war der Maximalschaden 5,8 Billionen Euro, nach Betaverteilung, Simulation und Extremwertstatistik beträgt er 5,9 Billionen Euro.
Da die gesamte Studie nur auf Annahmen beruht und die ausgewählten Expertenschätzungen für den Maximalschaden von 150 Milliarden Euro. bis knapp 6 Billionen Euro reichen, würde man ein entsprechend großes Intervall für die Unsicherheit erwarten.
Überraschend ist aber, dass die Streuung des Maximalschadens laut VL sehr klein ist, nämlich 60,7 Milliarden Euro, also nur 1 % des Erwartungswerts von 5,8 Billionen Euro. Als Datenbasis dafür dienen VL-eigene Schätzungen für die 17 deutschen Kernkraftwerke, die sich nur minimal voneinander unterscheiden (VL, S. 92):

Betaverteilung kaum unterscheidbar von Normalverteilung
Mit dem Erwartungswert und der Varianz dieser fiktiven Stichprobe wird eine Betaverteilung auf dem Intervall [0,150 6,363] bestimmt:
»Da ein nuklearer Katastrophenfall immer mit sehr hohen Schadenaufwänden verbunden ist und ein bestimmtes Schadenausmaß nicht unterschreitet, handelt es sich … offenbar um eine linksschiefe Verteilung … Die zweiparametrige Betaverteilung mit den Parametern α > 0 und β > 0 erfüllt diese Eigenschaft unter entsprechender Wahl der Parameter.« (VL, S. 83)
Es wird α=832 und β=90 ermittelt. Eine Betaverteilung mit diesen Parametern ist kaum unterscheidbar von einer Normalverteilung mit μ=5,7565 und σ=0,0607:
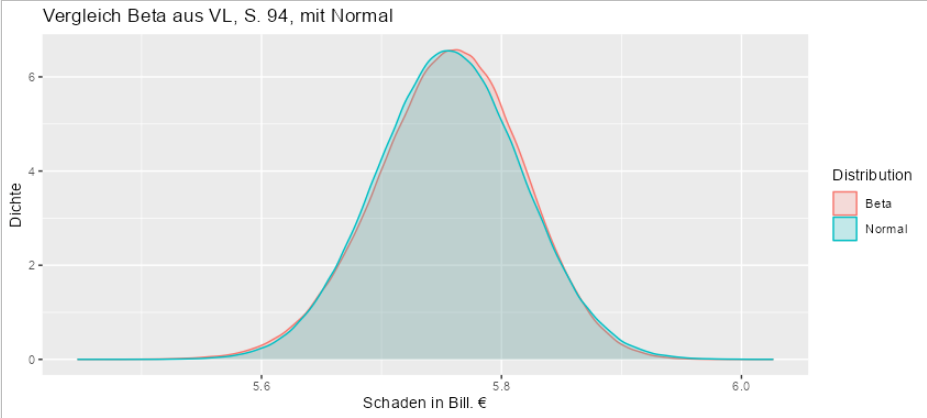
Offenkundig ist diese Verteilung nicht linksschief, sondern symmetrisch. Die Annahmen von VL werden durch die eigenen Daten widerlegt.
Anschließend wird auf den quasi-normalverteilten Daten mit einer sehr kleinen Streuung eine Extremwertverteilung simuliert. Die wendet man üblicherweise genau dann an, wenn eine Normalverteilung nicht passt und eine große Streuung zu erwarten ist. Nachdem die Standardabweichung der Extremwertverteilung (31,6 Milliarden Euro, S. 95) noch kleiner als in der Stichprobe ausfällt, beträgt die Prämie am Ende inklusive Risikozuschlag 6,09 Billionen Euro (5,9 + 6 × 0,0316 – der Faktor 6 ist willkürlich gewählt)
Mit den bereits vorher bekannten 5,8 Billionen Euro plus 5-facher Standardabweichung als Risikozuschlag wäre man in nur einer einzigen Zeile zum praktisch gleichen Ergebnis gekommen (5,765 + 5 × 0,0607 = 6,06), freilich ohne mit höherer Statistik zu glänzen.
Jahresprämie
Wie viel von diesen 6,09 Billionen Euro sind pro Jahr zu bezahlen? Um diese Frage zu beantworten, wird der Barwert betrachtet, also der Wert, den zukünftige Zahlungen in der Gegenwart haben. Die erste Größe zur Bestimmung der Jahresprämie ist die Eintrittswahrscheinlichkeit, die dem Deckungszeitraum entspricht. Bei einer Eintrittswahrscheinlichkeit von 1:1.000 ist der Deckungszeitraum 1.000 Jahre. Die zweite Größe ist der Bereitstellungszeitraum, also bis wann die 6,09 Billionen Euro bezahlt sein müssen: erst nach 1.000 Jahren oder schon nach 100? Die dritte Größe ist der verwendete Rechnungszins, der bei längeren Zeiträumen einen enormen Effekt haben kann.
Wenn man annimmt, dass die Prämie 1.000 Jahre lang gezahlt wird und der Rechnungszins 2 % beträgt, schrumpfen die 6,09 Billionen Euro auf 305,83 Euro pro Jahr und Kernkraftwerk zusammen (siehe VL S. 96, das Szenario Alterung 18x lassen wir der Einfachheit halber weg). Verringert man die Eintrittswahrscheinlichkeit vergleichsweise geringfügig auf 1:1.500 pro Jahr, reduziert sich die Jahresprämie von 305,83 Euro auf gerade mal noch 0,015 Euro (0,02 × 6,09 × 1012 / (1,021500 – 1)) Einen ebenso großen Hebel hat der Bereitstellungszeitraum. Soll die Prämie von insgesamt 6,09 Billionen Euro nicht nach 1.000, sondern bereits nach den ersten 50 Jahren bezahlt sein, steigt die Jahresprämie von 305,83 Euro auf 72 Milliarden Euro, bei 500 Jahren sinkt sie auf 6,1 Millionen Euro. 100 Jahre Bereitstellungszeitraum ergibt eine Jahresprämie von 19,5 Milliarden. Euro. Alle Zahlen stammen aus VL S. 97.
Größenordnung der Prämie von willkürlichen Annahmen abhängig
Aus heutiger Sicht ist diese Berechnung sogar noch großzügig, denn sie basiert auf einem Rechnungszins von 2 %, dem damaligen Höchstrechnungszins in der Lebensversicherung. Mit den aktuellen 0,25 % würde die Jahresprämie von 19,5 Milliarden Euro auf 53,7 Milliarden Euro steigen (0,0025 × 6,09 × 1012 / (1,0025100 – 1)).
Fazit: Die Jahresprämie hängt mit einem Faktor von mehreren Zehnerpotenzen von willkürlichen Annahmen zu Eintrittswahrscheinlichkeit, Bereitstellungszeitraum und Rechnungszins ab.
Risikoadäquate Haftpflichtprämie
Ist es eigentlich ökonomisch sinnvoll, Haftpflichtprämien für großindustrielle Risiken anhand des höchstmöglichen Schadens für alle möglichen Gefahren einschließlich Terror auszurechnen? De facto sind zahlreiche Branchen nur begrenzt versichert, also nicht nur Kernkraft, sondern beispielsweise auch Öl, Chemie oder Pharma.
1975 starben in Banqiao in China nach dem Bruch eines Staudamms etwa 200.000 Menschen, um Größenordnungen mehr als in allen bisherigen Nuklearunfällen zusammen. Folgt man der Logik von VL, sind deutsche Wasserkraftwerke drastisch unterversichert. Wenn Kernkraftwerke unbegrenzt gegen Terror versichert sein sollen, warum dann nicht auch die Stromnetzbetreiber, zum Beispiel gegen einen zweiwöchigen Blackout, der aus einem Cyberangriff auf das europäische Verbundnetz resultiert? Blackout ist ein Top-Risiko, sagen die Katastrophenämter. Nach dem Prinzip hypothetischer Höchstschäden müssten ganze Industriebranchen als nicht versicherbar deklariert werden.
Die Fokussierung auf den größtmöglichen Unfallschaden hat die absurde Konsequenz, dass Kohlekraftwerke problemlos versicherbar sind, obwohl sie jährlich für Millionen von Toten durch Luftverschmutzung sorgen. Nur sterben diese Menschen nicht durch einen Unfall, sondern durch den Regelbetrieb.
Die Berechnung einer risikoadäquaten Prämie darf sich deshalb nicht nur auf den hypothetischen Maximalschaden konzentrieren, sondern muss externe Kosten insgesamt betrachten und zwar einschließlich der Umweltfolgen und im Vergleich mit anderen Energieträgern. Schließlich ist das Risiko eines Unfalls abzuwägen gegenüber dem gesellschaftlichen Nutzen der Kernenergie, also der zuverlässigen, umweltverträglichen und CO₂-armen Stromerzeugung.
Zusammenfassung
Die Studie der Versicherungsforen Leipzig GmbH arbeitet mit willkürlichen Annahmen, unangemessenen Methoden und irrealen Spekulationen. Nur so kann sie ihr offenkundiges Ziel erreichen, völlig überhöhte Versicherungsprämien für Kernkraftwerke zu »errechnen« und Kernkraftwerke als »unversicherbar« zu brandmarken. Letztlich repliziert sie nur veraltete Arbeiten deutscher Ökonomen Ende der 1980er, Anfang der 1990er Jahre. Die Aufarbeitung des Tschernobyl-Unglücks durch internationale Behörden und wissenschaftliche Einrichtungen ignoriert VL, ebenso die Frage, ob ein Unglück wie in Tschernobyl in Deutschland überhaupt hätte passieren können. Das LNT-Modell ist mit viel zu großen Unsicherheiten behaftet, um damit Krebsfälle nach einem Nuklearunfall vorherzusagen. Die geschätzten Strahlendosen und die geschätzte Anzahl der Todesfälle entbehren jeder empirischen Grundlage. Die Eintrittswahrscheinlichkeit für einen Super-GAU ist unlogisch. Die statistischen Berechnungen beruhen ausschließlich auf fiktiven Daten und liefern keinen Mehrwert. Je nach Parametern lässt sich unabhängig vom Risiko jede beliebige Jahresprämie ausrechnen. Die einseitige und isolierte Betrachtung des hypothetischen Maximalschadens ist nicht risikoadäquat.
Quellen
- Berechnung einer risikoadäquaten Versicherungsprämie zur Deckung der Haftpflichtrisiken, die aus dem Betrieb von Kernkraftwerken resultieren; Benjamin Günther, Torsten Karau, Eva-Maria Kastner, Walter Warmuth; Versicherungsforen Leipzig; 2011-04-01
- Risiko Atomkraft Forscher errechnen horrende Haftpflicht-Kosten für AKW; Der Spiegel; 2011-05-11
- Risiko Atomkraft: Die teuerste Haftpflichtpolice der Welt; Manager-Magazin; 2011-05-11
- „Die DAV sieht die Atomkraft nicht als nachhaltig an“; Steffi Hüthig; Versicherungsjournal; 2022-01-27
- Nuclear operators’ third party liability amounts and financial security limits; OECD Nuclear Energy Agency; Februar 2019
- Aktualisierte Fassung: Nuclear Operators’ Liability Amounts and Financial Security Limits; OECD Nuclear Energy Agency; Juni 2022
- Safety of Nuclear Reactors; World Nuclear Association; März 2022
- ExternE – Externalities of Energy, Vol. 5: Nuclear; Europäische Kommission; 1995
- Does Imaging Technology Cause Cancer? Debunking the Linear No-Threshold Model of Radiation Carcinogenesis; Jeffry A. Siegel, James S. Welsh; Technology in Cancer Research & Treatment; 2015-03-30
- Die Empfehlungen der Internationalen Strahlenschutzkommission (ICRP) von 2007 – ICRP-Veröffentlichung 103, deutsche Ausgabe; Internationale Strahlenschutzkommission; März 2007
- Health effects due to radiation from the Chernobyl accident; United Nations Scientific Committee on the Effects of Atomic Radiation (UNSCEAR); 2008
- Tschernobyl: »Panik kann schlimmer sein als Strahlung«; Interview mit Prof. Geraldine Thomas; Nuklearia; 2020-04-25
- What are the safest and cleanest sources of energy?; Hannah Ritchie; Our World in Data; 2020-02-10
- A Case Study in how Junk Science is Used by Anti-Nuclear Environmentalists; Robert Wilson; Carbon Counter; 2015-06-05
Der Autor bedankt sich bei Rainer Klute für die kritische Durchsicht des Textes und die vielen wertvollen Hinweise.

Wolfgang Abele studierte Mathematik an der Universität Hamburg, ist Aktuar (DAV) und arbeitet bei einer Unternehmensberatung

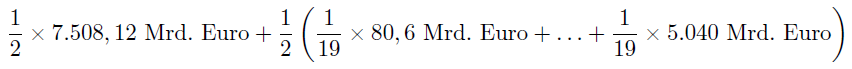
7 Antworten
Ich verstehe nicht, warum nicht stärker hinterfragt wurde, wie viel Radioaktivität bei einem GAU überhaupt frei werden kann. In allen deutschen Anlagen wird ein GAU beherrscht, das heißt, es dringt keine gefährliche Strahlung nach außen. Also gibt es auch keine Gefährdung, und damit kein Schaden in Billionenhöhe. Junk Science vom Feinsten.
Diese ganze Berechnung beruht doch nach meinem Verständnis auf der Annahme, ein Unglück wie Tschernobyl könne in einem Leichtwasserreaktor mit Containment passieren.
Fukushima zeigt ein anderes Bild. Auf eine dreifache Kernschmelze folgt eine sehr geringe Freisetzung von Radioisotopen.
Und das war ohne die Sicherheitsauslegung von deutschen Reaktoren wie Wasserstoffrekombinatoren und gefilterte Druckentlastung.
Der Bericht von UNSCEAR über Taiwan wurde nicht diskutiert. Danach haben Menschen mit geringer Strahlendosis seltener Krebs, als andere.
Was ist in Taiwan passiert?
Dort war Baustahl mit Kobalt-60 kontaminiert mit der Folge, daß die Bewohner ständig einer Ganzkörperbestrah-
lung durch harte Gamma-Strahlung ausgesetzt waren. Die Gebäude waren in 1982 / 1983 gebaut worden, die er-
höhte Gamma-Strahlung in Räumen wurde erst nach 10 Jahren in 1992 entdeckt. Man machte sich auf die Suche
nach weiteren kontaminierten Bauten und wurde fündig. Insgesamt hatte man ein Kollektiv von 10 000 Personen,
die über 9 bis 20 Jahre einem Strahlenpegel ausgesetzt waren, wie er weder in der Natur noch im Bereich der
Kerntechnik vorkommt. Anhand der gemessenen Ortsdosisleistung in den Gebäuden konnte man auf den Strahlen-
pegel von 1982 rückrechnen und mit dem Wohnverhalten der Leute die gesamte erhaltene Dosis abschätzen. Und
man konnte die Gesundheit der Bewohner beobachten. Hier die Daten von dem Teilkollektiv von 1100 Personen mit
der höchsten Dosis:
In 1983 betrug die mittlere Jahresdosis 74 mSv, und die maximale 910 mSv.
Die kumulierten Jahresdosen waren im Mittel 4 Sv, der Maximalwert 6 Sv.
Bei einer angenommenen Aufenthaltsdauer in den Wohnungen von 4000 Stunden im Jahr lag der
Strahlenpegel 1983 im Mittel bei 20 µSv/h und maximal bei 200 µSv/h.
Diese Zahlen sind so hoch, daß sie jedem Fachmann, der in Sachen Strahlen ausgebildet ist, erschaudern lassen.
In dem gesamten Kollektiv hätte es unter den Erwachsenen
186 Krebstodesfälle geben müssen.
Nach dem im Strahlenschutz angewandten LNT-Modell hätte es durch Strahlung weitere
56 Krebstodesfälle geben müssen.
Bisher wurden tatsächlich aber nur
5 Krebstodesfälle beobachtet.
Danke für die gute Darstellung. Gibt es hierzu auch zitierfähige Quellen? Dazu Inhalte: In vielen seriösen Publikationen und auch im Röntgen Museum wird eigentlich sehr klar, dass die Gesundheitsgefährdung durch Strahlung extrem überschätz wird. Ich wundere mich nur warum die Experten so erstaunlich stumm bleiben und immer der gleiche LNT Quatsch öffentlich diskutiert wir.
Die beschränkte Anwendbarkeit des LNT-Modells wird noch deutlicher im Absatz (161) der ICRP Publication 103 beschrieben (in deutscher Übersetzung durch das Bfs):
„(161) Die kollektive effektive Dosis ist ein Instrument zur Optimierung und zum Vergleich radiologischer Techniken und unterschiedlicher Strahlenschutzmethoden. Die kollektive effektive Dosis ist nicht als Instrument für epidemiologische Studien gedacht und ist ebenfalls nicht geeignet, um Risikoabschätzungen zu erstellen. Dies liegt daran, dass die Annahmen, die bei der Berechnung der kollektiven effektiven Dosis (z.B. bei Anwendung des LNT-Modells) impliziert werden, große biologische und statistische Unsicherheiten beinhalten. Kollektive effektiven Dosen, die auf sehr geringen Expositionen großer Bevölkerungsgruppen beruhen, können vernünftigerweise nicht verwendet werden, um durch Krebs verursachte Todesfälle zu berechnen. Dies soll vermieden werden, denn solche Berechnungen auf der Grundlage der kollektiven effektiven Dosis waren nie beabsichtigt. Sie sind biologisch wie auch statistisch sehr unsicher. Außerdem enthalten sie eine große Anzahl widersprüchlicher Daten, die oft nicht reproduziert werden können, wenn Abschät- zungen aus dem Zusammenhang gerissen werden. Deshalb stellen sie eine unzulässige Anwendung dieser Strahlenschutzgröße dar.“ – Diese Beschränkung wird auch von den zuständigen Behörden nicht bestritten. Es gibt insoweit in der Fachwelt also keinen Dissens.
Der Beitrag von Dr. Björn Peters ist vor allem kurz und wenn seine Voraussetzung nachprüfbar ist, wäre er überzeugend und machte die ganze „junk science“ überflüssig. Leider hat noch nirgendwo in der Welt m. W. ein solcher Versuch mit üblichen Reaktoren stattgefunden, nämlich, ob wirklich keine gefährliche Strahlung nach aussen dringt. Die Wahrscheinlichkeit und Murphy’s Gesetz sprechen eher dafür, dass hier – selbst in deutschen AKW – noch ein Risiko besteht. Nur bei Reaktoren mit TRISO Brennelementen und entsprechender Bauform kommt die „inhärente Sicherheit“ zum Tragen. Durch mehrere Versuche wurde dies auch bewiesen: die sogenannte „Selbstlöschung“ der Kugelbett-Technik. Sie wurde in Jülich entwickelt und nun in China fertiggestellt – soweit bekannt.
Gut, dass hier auch mal die LNT-Annahme aufs Korn genommen wird. Eine fake Theorie, wie sie in keinem Buche stehen sollte!