Einführung in die Reaktorphysik: Kapitel 1 – kernphysikalische Grundlagen

1.1 Aufbau der Materie

[math]!E = m c^2[/math]

Jede hat Einsteins berühmte Formel „Energie ist gleich Masse mal Lichtgeschwindigkeit zum Quadrat“ schon mal gesehen: Sei es als T-Shirt-Aufdruck, als Graffito oder als Musiktitel. Aber was bedeutet sie?

Sie verknüpft die Masse eines Körpers – seine Fähigkeit, sich Änderungen seines Bewegungszustands zu widersetzen bzw. in einem Gravitationsfeld ein Gewicht zu haben – über eine große Konstante, die quadrierte Lichtgeschwindigkeit, mit seinem Energiegehalt. Einem Energiezuwachs entspricht stets auch ein Massenzuwachs, einer Energieabgabe ein Massenverlust. Aufgrund des sehr großen Betrages [math]c^2 \approx 9 \times 10^{16} \, \mathrm{m}^2/\mathrm{s}^2[/math] führen dabei selbst sehr große Energieumsätze nur zu winzigen Massenänderungen und umgekehrt entsprechen kleinen Massenänderungen gewaltige Energiebeträge.

Aufgabe
Ein Akkumulator nehme eine Energiemenge von [math]W = 100 \, \mathrm{Wh}[/math] auf. Wie groß ist der Massenunterschied zwischen geladenem und leerem Akku?

Lösung
Es gilt:

[math]!W = 100 \, \mathrm{Wh} = 100 \times 3600 \, \mathrm{Ws} = 3.6 \times 10^5 \, \mathrm{J}[/math]

entsprechend einer Masse von:

[math]!m = W/c^2 = \frac{3.6 \times 10^5 \, \mathrm{J}}{9 \times 10^{16} \, \mathrm{m}^2/\mathrm{s}^2} = 4 \times 10^{-12} \, \mathrm{kg} = 4 \, \mathrm{ng}[/math]

In Worten: 4 Nanogramm = 4 Milliardstelgramm.

Kein Wunder, dass wir im Alltag diese Massenänderungen nicht bemerken!

Aber wie kann es überhaupt sein, dass Körper Energie speichern? Wie wird sie in der Materie absorbiert?

Betrachten wir ein alltägliches Kraftfeld: Z. B. das elektrische Feld zwischen den Polen des Akkumulators in obiger Aufgabe, oder auch das Feld eines Haushaltsmagneten. Nun stellen wir uns vor, wir könnten dieses Feld mit einem Schraubstock zusammenpressen. Immer enger, immer dichter packen wir es, bis wir die Größe der Atome erreicht haben: Jetzt ist das Feld so kompakt geworden, seine Energiedichte ist so enorm, dass es nicht mehr durchlässig ist, sondern die Beschaffenheit einer harten, undurchdringlichen Substanz angenommen hat.

Genau dies ist der Grund, warum die Tischplatte, auf der der Rechner steht, an dem ich diesen Artikel schreibe, fest und solide ist und sein Gewicht mühelos trägt: Die Atome, aus denen sie besteht – genauer gesagt: die Atomhüllen – enthalten starke, extrem verdichtete Kraftfelder, die gemeinsam einen steifen, undurchdringlichen Festkörper bilden.

Die Atome haben Ausdehnungen von größenordnungsmäßig 0.1 Nanometern. Ihr Volumen ist beinahe komplett mit starken elektromagnetischen Feldern ausgefüllt. Der winzige positiv geladene Kern im Zentrum mit einem Radius von einem Hunderttausendstel Nanometer und die negativen Elektronen, die in der Atomhülle verschiedenen Energieniveaus besetzen und dadurch die chemischen Bindungseigenschaften des Atoms bestimmen, beanspruchen nur einen minimalen Volumenanteil! Fast das gesamte Atom ist eine in etwa kugelförmige „Felderwolke“.

Sehr verbreitet ist die Aussage: Alle Substanzen bestehen vorwiegend aus leerem Raum – doch dies stimmt nicht! Denn Felder sind nicht „Nichts“! Sie bestehen aus einem Gebrodel von ständig entstehenden und vergehenden Botenteilchen, die man, da sie nur indirekt, z. B. durch den sogenannten Casimir-Effekt, nachweisbar sind, auch virtuelle Teilchen nennt. Das elektromagnetische Feld wird durch virtuelle Photonen vermittelt. Wird die Struktur des Feldes geändert, wandeln die virtuellen Teilchen sich in gewöhnliche um, und es wird Energie abgestrahlt, im Falle eines elektromagnetischen Feldes natürlich in Form elektromagnetischer Wellen, bzw. Photonen im Teilchenbild.

Nun kompaktieren wir unser Kraftfeld noch weiter, bis hinunter zum Kern in den Femtometer(= Millionstel Nanometer)-Bereich: Die Energiedichte steigt in schwindelnde Höhen. Wir erhalten ein fast infinitesimales Bündel gehärteter Felder, in dem genug Kraft konzentriert ist, um die Energiewandlungen der Sterne und die Kreativität der Menschen in Gang zu halten.

Der Atomkern hat etwa ein Zehntausendstel des Radius‘ der Atomhülle (zehn Femtometer vs. 0.1 Nanometer), und damit ein Billionstel ihres Volumens. Beinahe die komplette Masse des Atoms – und damit aller uns vertrauten Materie – ist in ihm konzentriert: Er besteht aus positiven Protonen und ungeladenen Neutronen. Sie weisen ungefähr die gleiche Masse auf: 1800 mal die des Elektrons. Warum die Elektronen in der Hülle bleiben, ist klar – sie sind negativ, so dass die positiven Protonen im Kern sie anziehen. Aber warum bleibt der Kern zusammen? Sollten die Protonen sich nicht gegenseitig abstoßen und davonfliegen? Die Antwort erhalten wir, indem wir noch eine Stufe tiefer gehen, und in die Kernteilchen, die Protonen und Neutronen, hineinsehen.

Protonen und Neutronen sind, im Gegensatz zu (wahrscheinlich) Elektronen, nicht elementar, sondern aus je drei Teilchen zusammengesetzt, die Murray Gell-Mann in Memoriam James Joyce‘ Quarks nannte, und die stets nur in „Paketen“ von zwei oder drei anzutreffen sind. Es existieren sechs verschiedene Quarks mit den Bezeichnungen up, down, strange, charm, top, und bottom (auch: beauty). Das Proton enthält zwei up- und ein down-Quark, das Neutron zwei down und ein up. Die Quarks tragen Bruchteile der elektrischen Elementarladung (=die Ladung, die mit positivem Vorzeichen in einem Proton, mit negativem in einem Elektron enthalten ist): Das up +2/3, das down -1/3, so dass das Proton die Ladung +1 und das Neutron die Ladung 0 hat.

Die Quarks haben jedoch zusätzlich zur elektrischen noch eine weitere Ladung bzw. Eigenschaft. Zusammengehalten werden sie durch eine Naturkraft, die, im Gegensatz zur elektromagnetischen oder der Gravitation nur eine extrem kurze Reichweite hat: Die sogenannte Farbkraft reicht kaum über den Rand der Protonen und Neutronen hinaus! Sie heißt so, weil für die zusätzliche Eigenschaft der Quarks die Bezeichnung „Farbe“ oder auch „Farbladung“ gewählt wurde. Damit lässt sich ihre Verteilung auf die drei Quarks innerhalb eines Kernteilchens anschaulich wiedergeben: Ein ganzes Proton oder Neutron hat keine Farbladung (es ist „weiß“), weswegen sich die additive Farbmischung (RGB-Signal beim Monitor) als Modell anbietet – von den drei Quarks muß je eines „rot“, eines „grün“ und eines „blau“ sein. Es gibt auch Antiquarks, die „Antifarben“ tragen. Farbe plus Antifarbe ergibt in dem Modell ebenfalls weiß, so dass auch Teilchen aus zwei Quarks möglich sind, die Mesonen.

Elektrische Ladungen üben Kräfte aufeinander aus, indem sie Felder aus virtuellen Photonen aufbauen – welche Teilchen übertragen das Farbkraft-Feld? Sie heißen Gluonen von Englisch „glue=Leim“, da sie die Protonen und Neutronen innerlich „zusammenkleben“. Und nun kommt die Überraschung: Die Masse des Kerns, die ja die fast die gesamte Masse der uns geläufigen Materie ausmacht, geht nur zu geringem Anteil (einige Prozent) von den Quarks, aus denen die Protonen und Neutronen bestehen, aus – sondern von dem Gluonenfeld zwischen den Quarks! Die rund 85 kg, die ich wiege, sind keine Materie, sondern Energie: Das ist der Gehalt von Einsteins berühmter Formel. Der größte Teil der Masse aller Objekte um uns herum ist in submikroskopisch kompakten Kraftfeldern gespeichert. Welche möchte, kann sich eine Vielzahl extrem kleiner, extrem stark gespannter Federn vorstellen, die überall in der Materie enthalten sind und die Materieteilchen – deren Beitrag zur makroskopisch sichtbaren Masse unbedeutend ist – miteinander verbinden. Die Federn innerhalb der Kerne bzw. Kernteilchen sind besonders stark gespannt: Deshalb ist fast die gesamte Masse und damit auch Energie der Materie hier konzentriert!

Während die Photonen als Feldteilchen der elektromagnetischen Kraft selbst keine elektrische Ladung tragen, verfügen die Gluonen über eine eigene Farbladung.

Die aufmerksame Leserin möchte mich jetzt fragen, wie denn Protonen und Neutronen im Kern zusammenbleiben, wenn die Farbkraft nur innerhalb jedes von ihnen wirkt? Die Antwort liegt in einem Regentropfen. Moleküle und Atome üben gewisse Kräfte auf Nachbarteilchen aus, obwohl sie jeweils als ganzes elektrisch neutral sind und – im Falle der Moleküle – die starken kovalenten Bindungskräfte nur innerhalb jedes einzelnen wirken: Starke Wasserstoffbrückenbindungen zwischen polaren Molekülen (z. B. Wasser) oder die schwächeren auf gegenseitiger Dipolinduktion beruhenden Van-der-Waals-Kräfte zwischen unpolaren Teilchen. Die Kletterhaftung des Geckos beruht auf Van-der-Waals-Anziehung wie auch die bei sehr tiefen Temperaturen auftretenden kristallinen Formen der Edelgase. Die stärkeren Wasserstoffbrückenbindungen halten die Doppelhelix der DNA-Moleküle zusammen und sorgen für den hohen Siedepunkt und die ausgeprägte Oberflächenspannung des Wassers – da die Moleküle sich gegenseitig anziehen, versucht ein Tropfen stets die Größe seiner Oberfläche zu minimieren, und bildet dadurch eine kugelförmige Gestalt aus.

Ein ähnliches Prinzip wirkt im Atomkern. Obwohl das Gluonenfeld primär innerhalb jedes Protons und Neutrons wirksam ist und dort jeweils die drei Quarks zusammenhält, leckt ein Rest der Farbkraft aus den Kernteilchen heraus und bindet sie aneinander, nicht völlig unähnlich den Wassermolekülen in einem Tropfen. Wir werden weiter unten sehen, dass die Interpretation des Kerns als Tropfen mit Oberflächenspannung die Ableitung einer nützlichen Näherungsformel für seine Bindungsenergie erlaubt!

Die Kraft, die zwischen Protonen und Neutronen wirkt, nennt man Starke Kernkraft oder einfach Starke Kraft. Die Leserin führe sich vor Augen, dass sie trotz ihrer immensen Stärke nur eine aus den Kernteilchen herausleckende Restkraft ist! Die Farbkräfte innerhalb der Protonen und Neutronen sind so stark, dass es gewaltige Teilchenbeschleuniger braucht, um sie zu untersuchen.

Aufgabe
Um welchen Faktor nimmt die Abstoßungskraft zwischen zwei Elementarladungen (e.g. Protonen) gleichen Vorzeichens zu, wenn ihr Abstand von 0.1 Nanometer ([math]10^{-10}[/math] Meter) auf 1 Femtometer ([math]10^{-15}[/math] Meter) verkleinert wird? Wie verhalten sich entsprechend die Energien, die benötigt werden, um sie aus sehr großer Entfernung bis auf einen Abstand von 0.1 Nanometer bzw. 1 Femtometer zusammenzuschieben?

Lösung
Die elektrostatische Abstoßung gehorcht dem Gesetz (klassische Näherung, quantenelektrodynamische Effekte vernachlässigt):

[math]!F_\mathrm{el} = \frac{1}{4 \pi \epsilon_0} \, \times \, \frac{Q_1 Q_2}{r^2}[/math]

mit der elektrischen Feldkonstanten [math]\epsilon_0 \approx 8.85 \, \times \, 10^{-12} \, \mathrm{As}/\mathrm{Vm}[/math] (Einheit Ampere-Sekunden pro Voltmeter), den beiden Ladungen [math]Q_1[/math] und [math]Q_2[/math] und dem Abstand [math]r[/math]. Da somit gilt [math]F_\mathrm{el} \propto r^{-2}[/math], steigt die Abstoßungskraft bei einer Verringerung des Abstandes um den Faktor [math]10^5[/math] auf das [math]10^{10}[/math]-fache (Zehn-Milliardenfache) an.

Die benötigte Energie (mechanische Arbeit), die man braucht, um sie aus dem Unendlichen auf einen endlichen Abstand [math]r[/math] zusammenzuschieben, berechnet sich durch Integration über Kraft mal Weg:

[math]!W(r) = \int_\infty^r F_\mathrm{el}(\hat{r}) \, \mathrm{d}\hat{r} \propto \int_\infty^r \frac{1}{\hat{r}^2} \, \mathrm{d}\hat{r} = [1/\hat{r}]_r^\infty = -1/r[/math]

Das Verhältnis der benötigten Arbeiten beträgt demnach

[math]!W(10^{-15} \, \mathrm{m})/W(10^{-10} \, \mathrm{m}) = 10^{-10}/10^{-15} = 10^5[/math]

Dieses Gedankenexperiment vernachlässigt die Kernkräfte: In Wirklichkeit würden die Protonen bei Unterschreiten eines bestimmten Abstandes beginnen, sich gegenseitig anzuziehen statt abzustoßen. Zusätzlich kämen Quanteneffekte ins Spiel, die wir später noch genauer betrachten werden. Präzise theoretische und experimentelle Untersuchungen zeigen: Die Bindungsenergien in Kernen sind um etwa eine Million mal größer als in der Atomhülle! Bei chemischen Reaktionen sind Energien von einigen Elektronenvolt pro Teilchen involviert, bei Kernereaktion Energien von einigen Mega-Elektronenvolt pro Teilchen.

Dabei ist das Elektronenvolt (Formelzeichen eV) die Energie, die eine Elementarladung (Elektron oder Proton) aufnimmt, wenn sie eine Spannung von einem Volt durchläuft. Es gilt [math]1 \, \mathrm{eV} \approx 1.602 \, 10^{-19} \, \mathrm{J}[/math]. In der Mikrophysik benutzen wir stets nur Elektronenvolt als Energiemaß – Joule ist keinesfalls gebräuchlich!

Nun wollen wir den Aufbau der Materie in einer Grafik zusammenfassen:

• Atomhülle: Ca. 0.1 Nanometer ausgedehnt. Enthält die – vermutlich punktförmigen(?) – negativ geladenen Elektronen auf verschiedenen Energieniveaus, wodurch das chemische Verhalten der Atome bestimmt wird. Chemische Reaktionen setzen Energien in der Größenordnung eines Elektronenvolts um.
• Atomkern: Ca. 10 Femtometer (ein Hunderttausendstel Nanometer) ausgedehnt. Enthält positiv geladene Protonen und elektrisch neutrale Neutronen. Diese Kernteilchen (auch genannt Nukleonen) sind rund 1800 mal massereicher als ein Elektron. Die Starke Kernkraft, die sie zusammenhält, ist eine „Leckkraft“, die auf die innerhalb von ihnen wirkende Farbkraft zurückgeht.
• Ein Proton besteht aus zwei up- und einem down-Quark, ein Neutron aus einem up und zwei down. Die Farbladungen der Quarks („rot“, „grün“ und „blau“) ergeben zusammen in „additiver Farbmischung“ stets weiß. Sie sorgen dafür, dass die Quarks durch das Gluonenfeld bzw. die durch es vermittelte Farbkraft aneinander gebunden werden. Fast die gesammte Masse der Materie steckt, entsprechend Einsteins berühmter Formel, in der Energie des Gluonenfeldes! Quarks und Elektronen tragen nur zu geringem Anteil bei: Die Masse der up- und down-Quarks ohne Gluonenfeld ist weniger als zehnmal größer als die Elektronenmasse!

Weblinks:

• The Scale of the Universe 2 – schön gemachte interaktive Animation, die es erlaubt, durch alle bekannten Größenmaßstäbe im Universum hindurchzuscrollen, von den Galaxiensuperhaufen bis zu den hypothetischen Strings als Bestandteile der Elementarteilchen.
• Powers of Ten – ein Trickfilm aus dem Jahr 1977, der auf eine Reise von alltäglichen Dingen bis zu fernen Galaxien und Quasaren und wieder zurück ins Kleinste, den subatomaren Bereich der Protonen, Neutronen und Quarks mitnimmt. Aus heutiger Sicht ist nicht alles korrekt dargestellt – so fehlt bei unserer Milchstraße zum Beispiel der Balken – aber der rund 9 Minuten lange Film ist dennoch äußerst sehenswert.

Ob Quarks und Leptonen (leichte Teilchen zu denen die Elektronen gehören) eine innere Struktur aufweisen, ist nicht bekannt. Manchen Theorien zufolge handelt es sich bei ihnen um Schwingungszustände von eindimensionalen Raumzeitfäden („Strings“).

Mithilfe von Einsteins Formel können wir die Masse von Elementarteilchen in der Einheiten MeV (Mega-Elektronvolt) pro Lichtgeschwindigkeit zum Quadrat ([math]\mathrm{MeV}/c^2[/math]) angeben.

Aufgabe
Die Leserin gebe die Massen von Elektron ([math]9.109 \times 10^{-31} \, \mathrm{kg}[/math]), Proton ([math]1.673 \times 10^{-27} \, \mathrm{kg}[/math]), Neutron ([math]1.675 \times 10^{-27} \, \mathrm{kg}[/math]) in der Einheit Mega-Elektronvolt durch Lichtgeschwindigkeit zum Quadrat an. Für die Lichtgeschwindigkeit soll der Wert [math]c = 2.998 \times 10^8 \, \mathrm{m}/\mathrm{s}[/math] benutzt werden.

Lösung
Es gilt

[math]!1 \, \mathrm{MeV}/c^2 = \frac{1.602 \times 10^{-13} \, \mathrm{J}}{(2.998 \times 10^8 \, \mathrm{m}/\mathrm{s})^2} \approx 1.782 \times 10^{-30} \, \mathrm{kg}[/math]

Durch Division ergibt sich:

• Elektron: [math]M_\mathrm{e-} \approx 0.511 \, \mathrm{Mev}/c^2[/math]
• Proton: [math]M_\mathrm{p+} \approx 938 \, \mathrm{Mev}/c^2[/math]
• Neutron: [math]M_\mathrm{n} \approx 940 \, \mathrm{Mev}/c^2[/math]

Die Masse des up-Quarks liegt im Bereich [math]1.7 … 3.1 \, \mathrm{MeV }/c^2[/math], die des down-Quarks bei [math]4.1 … 5.7 \, \mathrm{MeV }/c^2[/math].

1.2 Eigenschaften von Atomkernen

Ein Atomkern wird in erster Linie durch die Anzahl seiner Protonen und Neutronen beschrieben! Dies kennzeichnet ihn noch nicht völlig, ist gibt sogenannte Isomere die zwar die gleichen Teilchen enthalten aber unterschiedlich energetisch angeregt sind, aber für unseren Bedarf sind zunächst Masse und Ladung am wichtigsten.

Definition:

• Die Massenzahl des Kerns [math]A[/math] ist die Summe der Anzahl der Protonen [math]Z[/math] und der der Neutronen [math]N[/math]: [math]A = Z + N[/math].
• Die Kernladung (gemessen in Elementarladungen) ist natürlich identisch mit der Zahl der Protonen [math]Z[/math].
• Ein Nuklid ist eine bestimmte Kernart, gekennzeichnet durch [math]Z[/math] und [math]N[/math].
• Ein Element ist ein Kern mit einer bestimmten Protonenzahl [math]Z[/math]. Da ein Atom als ganzes neutral ist, ist die Zahl der Elektronen in der Hülle mit der der Protonen im Kern identisch. Jedes Element hat ein spezifisches chemisches Verhalten.
• Isotope sind Kerne mit gleicher Protonen- aber unterschiedlicher Neutronenzahl. Die meisten Elemente haben mehrere Isotope: So existieren Wasserstoffkerne mit einem Proton und keinem Neutron (leichter Wasserstoff), mit einem Proton und einem Neutron (Deuterium – schwerer Wasserstoff), und einem Proton und zwei Neutronen (Tritium – überschwerer Wasserstoff). Unterschiede im chemischen Verhalten verschiedener Isotope eines Elementes sind äußerst minimal sofern überhaupt messbar.
• Isotone sind Kerne mit unterschiedlicher Protonen- aber gleicher Neutronenzahl. Das Wort wurde übrigens gebildet, indem das „p“ wie Proton in „Isotop“ durch „n“ wie Neutron ersetzt wurde.
• Isobare (gr. barýs = „schwer“) sind Kerne gleicher Massenzahl [math]A[/math] (nicht zu verwechseln mit den Linien gleichen Drucks in der Meteorologie).

Die gebräuchliche Schreibweise für Nuklide ist:

[math]!^A_ZX[/math]

wobei für [math]X[/math] das Symbol des jeweiligen Elements eingesetzt werden muss. Die tiefgestellte Protonenzahl kann daher ggf. auch weggelassen werden, da ja aus dem Elementnamen bereits klar ist, wieviele Protonen vorhanden sind. Im laufenden Text können wir auch die Massenzahl direkt hinter das Elementsymbol schreiben: Z. B. C12 für das häufigste Kohlenstoffisotop [math]^{12}_6C[/math]. Manche Nuklide haben auch eigene Symbole: Beispielsweise existiert für Deuterium [math]^2_1H[/math] das Symbol D und für Tritium [math]^3_1H[/math] das Symbol T. Entsprechend nennt man den Deuteriumkern auch „Deuteron“ und den Tritiumkern „Triton“, obwohl bei letzterem mythologische und astronomische Verwechslungsgefahren gegeben sind.

Der einfachste mögliche Kern ist das Proton, Kern des leichten Wasserstoffs! Alle schwereren Kerne enthalten sowohl Protonen wie Neutronen, ein reiner Protonenkern wäre nicht stabil, da die Protonen sich gegenseitig trotz Starker Kraft zu sehr abstoßen würden – ungeladene Neutronen müssen als „Kitt“ dazwischensitzen. Je schwerer ein Kern ist, desto höher muss der Neutronenanteil sein. Es sei bemerkt, dass Neutronensterne, kompakte Sternreste, die bei Supernovaexplosionen mittelschwerer Sterne entstehen (sehr schwere werden zu Schwarzen Löchern, leichtere so wie unsere Sonne explodieren nicht sondern werfen ihre äußeren Schichten langsam als planetarischer Nebel ab und hinterlassen einen Weißen Zwerg), als überdimensionale Atomkerne von rund 30 km Durchmesser angesehen werden können, die ausschließlich aus Neutronen bestehen. Dies ist möglich, weil bei diesen Objekten außer nuklearen auch gravitative Kräfte eine wichtige Rolle spielen.

Aufgabe
Warum ist die Masse eines Atomkerns nicht einfach gleich der Summe der Masse seiner Protonen plus der der Neutronen? Ist er leichter oder schwerer?

Lösung
Im Kern sind die Protonen und Neutronen so extrem nah beieinander, dass sie sich gegenseitig sehr stark anziehen. Bringt man sie aus größerer Entfernung zusammen, muss man zuerst ihre gegenseitige Abstoßung überwinden, also Arbeit verrichten. Sind sie sich aber bis auf typische Kerndimensionen (10 Femtometer) nahegekommen, überwiegt die Anziehung durch die starke Kernkraft: Die Teilchen werden aufeinander zu beschleunigt, so dass Energie frei wird (ähnlich einer Feder, die erst auseinandergezogen ist und dann losgelassen wird) – mehr als zur Annäherung nötig war. Der Kern ist daher Einsteins Energie/Massenformel zufolge leichter als die Massensumme seiner Bestandteile. Die freigesetzte Energie nennt man Bindungsenergie.

Atommassen (es ist üblich, mit ganzen Atomen zu rechnen, also die Massen der Elektronen und der Feldenergie der Atomhülle miteinzubeziehen) werden meist in der Einheit Atomic Mass Unit (AMU, Formelzeichen u) angegeben, die einem Zwölftel der Masse eines Atoms des Kohlenstoffisotops C12 entspricht (und somit in etwa der Masse eines Protons oder Neutrons). Es gilt:

[math]!1 \, \mathrm{u} \approx 1.66054 \, \times \, 10^{-27} \, \mathrm{kg} \approx 931.49406 \, \mathrm{MeV}/c^2[/math]

Ein leichtes Wasserstoffatom wiegt [math]m_H = 1.007825 \, \mathrm{u}[/math] und ein Neutron [math]m_n = 1.008665 \, \mathrm{u}[/math].

Aufgabe
Wie groß ist die Bindungsenergie eines Heliumskerns He4 mit zwei Protonen und zwei Neutronen (Z=N=2)? Die Atommasse von He4 beträgt 4.0026 u.

Lösung
Es muss die Massendifferenz zwischen den Bestandteilen des Kerns und dem kompletten Kern berechnet werden:

[math]!\Delta M = Z \times m_H \, + \, N \times m_n \, – \, 4.0026 \, \mathrm{u} = 0.03 \, \mathrm{u}[/math]

Da wir die Masse des Heliumatoms einsetzen, muss auch die Masse des Wasserstoffatoms in der Formel benutzt werden und nicht die des Protons!

Der Massendifferenz (auch genannt Massendefekt) entspricht die Bindungsenergie

[math]!W_B = \Delta M \times 931.5 \, \mathrm{MeV}/\mathrm{u} = 27.95 \, \mathrm{MeV}[/math]

Es werden insgesamt rund 28 MeV frei, bzw. 7 MeV pro Kernteilchen. Diese Reaktion ist die Energiequelle der Sonne und anderer Hauptreihensterne (und damit letztlich der Motor der klassischen Erneuerbaren mit Ausnahme von Geothermie und Gezeiten). In der Sonne werden netto jeweils vier Protonen zu einem Heliumkern zusammengefügt, wobei zwei sich in Neutronen umwandeln.

Die Bindungsenergie pro Nukleon ist eine sehr wichtige Größe: Sie gibt an, wie stark ein Kern durch seine inneren Kräfte zusammengehalten wird, wie stabil er ist. Tragen wir sie in einem Diagramm über der Kernmasse auf, lässt sich etwas interessantes beobachten:

Von kleinen Massenzahlen her kommend steigt die Bindungsenergie pro Nukleon zunächst steil an, wobei He4 deutlich als lokales Stabilitätsmaximum erkennbar ist. Bei mittleren Atomgewichten verläuft die Kurve flacher, erreicht in der Nähe von Eisen ihr Maximum und fällt danach leicht ab. Wie können wir dieses Verhalten deuten?

Erinnern wir uns daran, dass Kerne eine gewisse Verwandtschaft mit Wassertropfen aufweisen: Die Starke Kraft wirkt, als aus den Nukleonen heraustretender Rest der in ihrem Inneren wirkenden Farbkraft, ähnlich wie die intermolekularen Kräfte, die die Oberflächenspannung hervorrufen. Diese Ähnlichkeit des physikalischen Mechanismus können wir nutzen, um ein einfaches Kernmodell herzuleiten!

Wir sehen am Verlauf der Kurve, dass die Kräfte zwischen den Nukleonen nur zwischen benachbarten Teilchen wirksam sind (so kurzreichweitig sind sie!). Denn wenn im Kern jedes auf jedes wirken würde, wäre die Gesamtbindungsenergie proportional zu [math]A^2[/math], die Bindungsenergie pro Teilchen demnach proportional zu [math]A[/math]: Die Kurve steigt jedoch nicht immer weiter an sondern flacht ab einer gewissen Massenzahl ab. Das bedeutet, dass die Gesamtenergie proportional zu [math]A[/math] und die Energie pro Teilchen somit näherungsweise konstant sein muß – jedes Teilchen also nur seine unmittelbaren Nachbarinnen anzieht.

Die Kernkräfte liefern demnach einen Energiebeitrag von:

[math]!W_1 = a_1 \times A[/math]

Die Nukleonen an der Kernoberfläche werden jedoch nur von halb so vielen Nachbarteilchen angezogen wie die tief im Inneren, dies entspricht der Oberflächenspannung eines Flüssigkeitstropfens. Es muss somit ein negativer Term hinzugefügt werden:

[math]!W_2 = -a_2 \times F[/math]

wobei die Oberfläche [math]F \propto V^{2/3}[/math] dem Volumen hoch zwei Drittel proportional ist. Das Volumen widerum ist in guter Näherung direkt proportional der Massenzahl [math]V \propto A[/math]. Damit erhalten wir

[math]!W_2 = -a_2 \times A^{2/3}[/math]

Obwohl bei größeren Kernen ein Neutronenüberschuss die Gesamstabilität unterstützt, senkt ein Ungleichgewicht zwischen Neutronen- und Protonenzahl die Bindungsenergie, da Neutronen und Protonen die Neigung haben, sich mangels Abstoßungskraft paarweise stark aneinander zu binden – es entstehen im Kern quasi Deuteronen als „Subkerne“. Teilchen, die nicht solcherart verpartnert werden können, sind weniger stark gebunden. Die Differenz von Neutronen- und Protonenzahl ist [math]N-Z = A – Z – Z = A – 2Z[/math]. Der die Bindungsenergie senkende Asymmetriefaktor lautet damit

[math]!W_3 = -a_3 \times \frac{(A-2Z)^2}{A}[/math]

Und natürlich stoßen die Protonen sich gegenseitig ab! Die potentielle Energie der elektrostatischen Kraft ist proportional zu [math]Z^2/R \propto Z^2/A^{1/3}[/math]:

[math]!W_4 = -a_4 \times \frac{Z^2}{A^{1/3}}[/math]

Jedes Nukleon hat einen Eigendrehimpuls („Spin“), der ihm ein eigenes Magnetfeld verleiht, es zu einem winzigen Dipol (analog Stabmagnet) werden lässt – auch die Neutronen, da diese zwar als ganzes neutral sind, aber geladene Komponenten (die Quarks) enthalten, die ein Magnetfeld aufbauen können, ähnlich wie ein im ganzen neutrales Atom ein magnetisches Moment haben kann. Magnetische Dipole ziehen sich gegenseitig an (zwei Stabmagnete jeweils Nordpol an Sübpol zusammenlegen!), daher herrscht auch zwischen den Kernteilchen eine paarweise magnetische Anziehung, und zwar jeweils zwischen Proton und Proton sowie Neutron und Neutron. Dies bedingt einen weiteren Term:

[math]!W_5 = \pm a_5 \times A^{-3/4}[/math]

Der Exponent -3/4 wird empirisch gewonnen, als Vorzeichen ist zu wählen:

• Gerade Protonen- und gerade Neutronenzahl (g/g-Kern): [math]+[/math]
• Gerade Protonen- und ungerade Neutronenzahl (g/u-Kern): [math]a_5 = 0[/math]
• Ungerade Protonen- und gerade Neutronenzahl (u/g-Kern): [math]a_5 = 0[/math]
• Ungerade Protonen- und ungerade Neutronenzahl (u/u-Kern): [math]-[/math]

Die Konstanten [math]a_{1…5}[/math] lassen sich aus Experimenten und theoretischen Überlegungen ermitteln. Es ergibt sich für die Bindungsenergie die Bethe-Weizsäcker-Formel:

[math]!W_B \, / \, \mathrm{MeV} = \left( \Sigma_{i=1}^5 W_i \right) \, / \, \mathrm{MeV} = 15.76 \, A \, – \, 17.81 \, A^{2/3} \, – \\ 23.702 \times \frac{(A-2Z)^2}{A} \, – \, 0.711 \times \frac{Z^2}{A^{1/3}} \, \pm \, 34 \, A^{-3/4}[/math]

wobei der letzte Term für (g/u)- und (u/g)-Kerne wegfällt.

Für Kernmassenzahlen größer als 30 liefert dieses sogenannte Tröpfchenmodell erstaunlich gute Ergebnisse – die Abweichungen von experimentellen Werten liegen unter 1%.

Aus der Formel können wir ableiten, warum die Bindungsenergie pro Nukleon erst ansteigt und zu großen Massenzahlen hin wieder abfällt: Die starke anziehende Kernkraft reicht, da sie eine Leckkraft ist, von jedem Kernteilchen zu seinen Nachbarinnen. Dies bedeutet, dass die Stabilität des Kerns nur bis zu einem gewissen Punkt (Eisen 56) durch das Hinzufügen weiterer Teilchen gesteigert werden kann. Danach senkt jedes neu hinzukommende die Stabilität durch wachsende elektrostatische Abstoßung ([math]W_4[/math]). Damit große Kerne überhaupt stabil bleiben können, ist ein immer größerer Neutronenanteil als „Klebstoff“ nötig – dies führt jedoch aus „Sicht“ des einzelnen Nukleons zu einer weiteren Senkung der Bindungsenergie, da Neutronenüberschuss die Möglichkeit, stabile p-n-Paare zu bilden, verringert.

Der massereichste Kern, der so stabil ist, dass er auf der Erde natürlich in größeren Mengen vorkommt, ist Uran 238. Schwerere Nuklide müssen künstlich erbrütet werden.

1.3 Instabile Kerne und Radioaktivität

Auf dem Gipfel eines Berges sei eine flache Mulde, und darin rolle eine Kugel hin und her: So kann man sich einen instabilen Kern vorstellen. In der Welt der klassischen Physik wäre es völlig unmöglich, dass die Kugel den stabileren Zustand unten im Tal erreicht, denn sie ist in der Mulde auf dem Gipfel gefangen. Die Quantenphysik hingegen eröffnet diese Möglichkeit! Denn die Elementarteilchen haben die aus unserer makroskopischen Sicht bizarr anmutende Eigenschaft, nicht auf einen bestimmten Zustand festgelegt sein zu müssen, sondern sich mit einer gewissen Wahrscheinlichkeit in diesem und gleichzeitig mit einer gewissen Wahrscheinlichkeit in jenem befinden zu können. Eine quantenmechanische Kugel ist nicht in der Mulde, so wie eine makroskopische, sondern beispielsweise mit 80%iger Wahrscheinlichkeit in der Mulde und mit 20%iger außerhalb, auf dem Berghang, wo sie in den stabileren Zustand hinabrollen kann.

Wie das genau vor sich geht, können wir am besten erfassen, indem wir konkrete Zerfallsprozesse betrachten. Die beiden verbreitetsten Zerfallsarten sind Alpha- und Betazerfall. Der Alphazerfall ist eine spontane Kernspaltung – der Kern zerplatzt in zwei kleinere, alle Nukleonen bleiben erhalten – bei der einer der beiden Tochterkerne ein He4-Kern ist (schnelle He4-Kerne sind als Alphateilchen bekannt). Der Betazerfall ist anderer Natur: Er wird durch eine Naturkraft ausgelöst, die man, da sie deutlich schwächer als die Kernkraft ist, Schwache Kraft nennt. Diese kann Protonen und Neutronen ineinander umwandeln. Das Proton zerfällt dabei nach der Formel

[math]!p \longrightarrow n + e^+ + \nu_e[/math]

in ein Neutron, ein Positron (das positive Antiteilchen des Elektrons – schnelle Elektronen und Positronen werden als Betastrahlung bezeichnet) sowie ein Elektron-Neutrino, ein extrem massearmes (wenn auch höchstwahrscheinlich nicht völlig masseloses) Teilchen, das mit Materie kaum wechselwirkt und überschüssige Energie und Drehimpuls fortträgt. Neutrinos sind in der Tat so „wechselwirkungsimmun“, dass eine mehrere Lichtjahre dicke Bleiwand nötig wäre, um eines mit substantieller Wahrscheinlichkeit aufzuhalten.

Neutronen betazerfallen folgendermaßen:

[math]!n \longrightarrow p + e^- + \bar{\nu_e}[/math]

– es entsteht ein Proton, ein Elektron und ein Antielektronneutrino. Interessant ist, dass Neutronen nur im Inneren von Kernen längerfristig stabil sind, freie Neutronen zerfallen schon nach durchschnittlich 15 Minuten.

Es sind auch inverse Betazerfälle möglich, bei denen ein Proton ein Elektron aus der Atomhülle einfängt und in ein Neutron umgewandelt wird.

Können Kerne auch einzelne Nukleonen aussenden? Die meisten nicht: die benötigte Schwellenenergie ist zu hoch, im Bereich der Bindungsenergie der Teilchen von 8 MeV. Alphateilchen tragen dagegen bereits eine größere Portion Bindungsenergie in sich selbst und können dadurch leichter entkommen.

Ein Kern kann jedoch durch externe Einwirkung – Bestrahlung mit Teilchen – in einen angeregten Zustand versetzt werden: Dann ist genug Energie vorhanden, dass die Emission einzelner Nukleonen möglich ist. Die zusätzliche Energie kann aber auch in elektromagnetischer Form (Gammastrahlung) abgestrahlt werden.

Die Abgabe von Neutronen aus hochangeregten Kernen ist, wie wir später sehen werden, für die Steuerbarkeit von Kernreaktoren von höchster Bedeutung.

Wie kommen die Teilchen aus dem Kern heraus, obwohl die Starke Kernkraft sie festhält? Folgendes Diagramm zeigt die Situation am Beispiel des Alphazerfalls:

Es gibt Hinweise darauf, dass das Alphateilchen schon vor dem Zerfall im Mutterkern als kompakte Einheit existiert, da He4 sehr stabil ist. Es pendelt zunächst im Kern hin und her und prallt immer wieder gegen die Wände des Potentialtopfes, der von der Kernkraft verursacht wird. Ein klassisches, Newton’sches Teilchen käme nie und nimmer heraus! Aber in der Quantenmechanik sind Teilchen nicht hundertprozentig auf einen bestimmten Zustand festgelegt, es ist prinzipiell nicht möglich zu sagen: „Das Alphateilchen ist exakt da und da“. Es ist nur die Aussage möglich: „Mit dieser und jener Wahrscheinlichkeit befindet es sich in einem gewissen Raumbereich“! Dies wird durch die Schrödinger’sche Wellenfunktion [math]\Phi(\vec{x},t)[/math] beschrieben. Die Wahrscheinlichkeit, dass das Teilchen in einem Teilvolumen [math]V[/math] angetroffen wird, berechnet sich aus dem Raumintegral über das Betragsquadrat der Wellenfunktion:

[math]!P_\mathrm{Teilchen \, in \, V} = \iiint\limits_V |\Phi(\vec{x},t)|^2 \, \mathrm{d}x \, \mathrm{d}y \, \mathrm{d}z[/math]

Die Wellenfunktion sollte so normiert sein, dass das Integral über den gesamten Raum 1 ergibt – schließlich muß das Teilchen irgendwo sein!

Hieraus folgt, dass wenn das Teilchen in die Nähe des Potentialwalles der Kernkraft kommt, es sich mit einer gewissen Wahrscheinlichkeit bereits außerhalb befindet: die Wellenfunktion „ragt“ ein kleines Stück aus dem Kern heraus. Da das Teilchen ständig in dem Kern herumvibriert, prallt es immer wieder gegen den Wall, bis es sich rein zufällig außerhalb des Kerns wiederfindet und von der dort überwiegenden elektrostatischen Abstoßung fortgeschleudert wird! Diesen Prozess nennt man Tunneleffekt, da das Teilchen unter der Potentialbarriere „hindurchtunnelt“, wohingegen ein klassisches Teilchen oben drüber klettern müsste.

Der Tunneleffekt kann auch positiv geladenen Teilchen dabei helfen, gegen die elektrostatische Abstoßung in einen Kern einzudringen.

Interessant wird es, wenn, wie es in der Realität ja meist der Fall sein wird, sehr viele Atomkerne gleicher Art beisammen sind. In jedem davon prallt das Teilchen ständig gegen den Potentialwall, und bei jedem Anprall kommt es mit einer gewissen Wahrscheinlichkeit zum Zerfall. Daraus folgt, dass die Zahl der Kerne, die pro Zeiteinheit zerfällt, der Gesamtzahl der anwesenden Kerne proportional ist! Denn sie sind alle identisch, und je mehr vorhanden sind, desto größer die Wahrscheinlichkeit, dass zu einem bestimmten Zeitpunkt einer davon zerfällt. Dies lässt sich durch folgende Formel ausdrücken:

[math]!\mathrm{d}N = -\lambda \, \times \, N \, \mathrm{d} t[/math]

In Worten: Die zeitliche Abnahmerate ist der Zahl der anwesenden Kerne [math]N(t)[/math] proportional mit der Proportionalitätskonstanten [math]\lambda[/math] die auch Zerfallskonstante heißt. Dieses Gesetz gilt universell für alle Arten von Kernzerfällen.

Aufgabe
Die Leserin zeige, dass die Kernanzahl [math]N[/math] im Laufe der Zeit exponentiell abklingt.

Lösung
Eine Naturwissenschaftlerin würde augenblicklich sagen: Das ist offensichtlich! und die Aufgabe durch „Draufsehen“ als gelöst betrachten. Wir wollen jedoch aufschlüsseln, warum dies so ist.

Durch Umstellen erhalten wir:

[math]!\frac{\mathrm{d} N}{N} = -\lambda \, \mathrm{d} t[/math]

wir führen das Zeitintegral von [math]0[/math] bis [math]t[/math] durch

[math]!\int_{N(0)}^{N(t)} \mathrm{d} N / N = – \lambda \int_0^t \mathrm{d} \hat{t}[/math]

welches ergibt

[math]!\ln{[ N(t) ]} \, – \, \ln{[ N(0) ]} = -\lambda t[/math]

bzw.

[math]!\ln{\left( \frac{N(t)}{N(0)} \right)} = -\lambda t[/math]

und da die Exponentialfunktion die Umkehrfunktion zum natürlichen Logarithmus ist:

[math]!N(t) = N(0) \, \times \, \exp{\left(- \lambda t\right)}[/math]

Aufgabe
Es soll die Zeit [math]t_{1/2}[/math], nach der die Anfangsmenge [math]N(0)[/math] auf die Hälfte [math]N(0)/2[/math] abgenommen hat, als Funktion der Zerfallskonstanten [math]\lambda[/math] ausgedrückt werden.

Lösung
Es gilt

[math]!N(t_{1/2}) = N(0)/2 = N(0) \, \times \, \exp{\left(- \lambda t_{1/2}\right)}[/math]

woraus durch Logarithmierung folgt

[math]!\ln{(1/2)} = -\lambda \, t_{1/2}[/math]

und

[math]!t_{1/2} = \frac{\ln{(2)}}{\lambda} \approx \frac{0.693}{\lambda}[/math]

Die Halbwertszeit [math]t_{1/2}[/math] (Abk. HWZ) ist das gebräuchlichste Maß für die Geschwindigkeit radioaktiver Zerfälle. Künstliche, überschwere Nuklide können Halbwertszeiten von Sekundenbruchteilen haben, bei anderen Kerne liegen sie im Bereich von Jahrmilliarden – und natürlich existiert auch alles dazwischen! Genaugenommen gibt es übrigens keine absolut stabilen Kerne. Mit einer extrem geringen Wahrscheinlichkeit zerfällt auch ein Eisen 56-Kern, nur sie ist eben so niedrig, dass die Halbwertszeit unmeßbar lang, um Zehnerpotenzen größer als das Alter des Universums ist.

Obwohl die einzelnen Zerfallsereignisse vom Zufall bestimmt werden, ergibt sich bei einer großen Anzahl von Kernen ein völlig determiniertes Verhalten: Dies entspricht den Gesetzen der Thermodynamik – die Bewegungen der einzelnen Moleküle sind rein zufällig, aber Wärme strömt stets vom heißen zum kalten Körper und nicht umgekehrt. Prinzipiell ist auch die andere Richtung möglich, doch ist dies unvorstellbar unwahrscheinlich. Genauso wäre es prinzipiell denkbar, dass eine Probe von einem instabilen Nuklid langfristig erhalten bleibt ohne zu zerfallen, oder dass eine stabile Substanz blitzschnell zerfällt – nur ergibt sich aus der Stochastik, dass ein solches Ereignis einem „thermodynamischen Wunder“ gleichkäme, es also mit beinahe absoluter Sicherheit nie beobachtet werden wird.

Welche Kerne sind stabil, welche instabil? Die Nuklidkarte, auf der die Protonen- über der Neutronenzahl der Kerne aufgetragen ist, zeigt es:

Weblink: Interaktive Nuklidkarte mit Atomdaten

Wir erkennen, dass mit zunehmender Kernmasse das Verhältnis Neutronen/Protonen der Kerne anwächst – die Nuklide biegen unter die Diagonale ab – da immer mehr Neutronen benötigt werden, um den Kern entgegen der elektrostatischen Abstoßung der Protonen zu binden. Auch fällt auf, dass bei den meisten Kernen der Betazerfall der bevorzugte Prozess ist: Die Starke Kraft wirkt ja nicht auf Elektronen/Positronen oder Neutrinos, so dass es deutlich einfacher ist, diese freizusetzen als Alphateilchen. Durch Beta-Plus-Zerfall (Proton zu Neutron) rücken die Nuklide bei gleichbleibender Massenzahl schräg von links oben nach rechts unten auf den schwarzen Stabilitätsbereich zu, Beta-Minus-Zerfall (Neutron zu Proton) lässt sie analog von rechts unten nach links oben wandern.

Der Alphazerfall kommt vorwiegend bei sehr schweren, instabilen Kernen vor, bei denen die Coulomb-Abstoßung so stark ist, dass die Emission von Heliumkernen wahrscheinlich wird. Hierbei nimmt die Massenzahl um 4 ab, das Nuklid rückt parallel zur Winkelhalbierenden (N=Z) nach links unten auf den Ursprung zu.

1.4 Spaltung und Fusion

Der radioaktive Zerfall lässt sich so weit wir heutzutage wissen nicht extern beeinflussen: Die Zerfallswahrscheinlichkeit eines Kerns hängt nur von den Wellenfunktionen in seinem Inneren ab. Es ist kein Mittel bekannt, diese von außen zu manipulieren um beispielsweise die Zefallsrate und dadurch die Energiefreisetzung zu steigern. Wir möchten Kerne jedoch effizient und steuerbar als Energiequelle nutzen. Daher müssen wir sie aktiv durch Teilchenbestrahlung zur Freisetzung ihrer Bindungsenergie anregen.

Welche Möglichkeiten es hierzu gibt, verrät ein Blick auf die Bindungsenergiekurve: Der am stärksten gebundene Kern ist Eisen 56. Die beim Zusammenfügen des Kerns aus einzelnen Nukleonen pro Teilchen freiwerdende Energie ist bei ihm am höchsten: Daher können wir immer dann Energie freisetzen, wenn wir uns auf das Eisen zu bewegen – indem wir Kerne, die leichter sind, miteinander verschmelzen oder solche die schwerer sind spalten, in kleinere Bruckstücke zerlegen. Das Eisen ist in dieser Hinsicht das Meer der Kernphysik: das Minimum der potentiellen Energie, das Maximum an Stabilität.

Aufgabe
Wieviel Energie wird frei, wenn ein Proton und ein Bor-11-Kern zu drei Helium-4-Kernen reagieren?
Atommassen: Wasserstoff: 1.0078 u, Bor 11: 11.0093 u, Helium 4: 4.0026 u.

Reaktionsgleichung:

[math]!^1H \, + \, ^{11}B \longrightarrow 3 \, ^4He[/math]

Lösung
Wieder stellen wir im Geiste von Einsteins Formel die Massenbilanz (Masse nach Reaktion minus Masse vor Reaktion) auf, um auf die Energiebilanz schließen zu können:

[math]!\Delta M / \mathrm{u} = 3 \times 4.0026 \, – \, (11.0093 + 1.0078) = -0.0093[/math]

da 1 u einer Energie von 931.5 Mev entspricht, wird folgender Energiebetrag freigesetzt:

[math]!\Delta W = 0.0093 \times 931.5 \, \mathrm{MeV} \approx 8.7 \, \mathrm{MeV}[/math]

Aus Sicht des Bor-11-Kerns erfolgt bei dieser Reaktion übrigens keine Bewegung in Richtung des Stabilitätsmaximums Eisen, sondern in die Gegenrichtung, hin zum leichteren Helium. Es kann dennoch Energie freigesetzt werden, da das Helium 4 ein ungewöhnlich stabiler Kern ist, der als lokales Maximum der Bindungsenergiekurve über die anderen leichten Nuklide hinausragt.

Die obige H-B11-Reaktion ist eine sogenannte „aneutronische Fusionsreaktion“ – sie setzt keinerlei Neutronen frei, was sie als Energiequelle attraktiv macht, da die entstehenden Alphateilchen zum einen die Reaktorhülle nicht aktivieren (d.h. das Material nicht in radioaktive Nuklide transmutieren), zum anderen dank ihrer Ladung durch elektromagnetische Felder gelenkt werden und direkt Elektrizität erzeugen können ohne Umweg über Kühlkreisläufe und Turbogeneratoren.

Kerne verschmelzen nicht einfach so: Sie sind positiv geladen, und stoßen sich daher so lange mit großer Kraft ab, bis sie sich nahe genug gekommen sind, dass die anziehende Kernkraft überwiegt. Sie müssen, damit Fusion eintritt, mit sehr großer Geschwindigkeit zusammenstoßen. Das letzte Stückchen Annäherung wird dabei vom Tunneleffekt übernommen.

Es gibt verschiedene Ansätze, die Kerne mit ausreichender Kraft kollidieren zu lassen. Bei den meisten heutigen Fusionsexperimenten werden die Substanzen, die zur Reaktion gebracht werden sollen – Deuterium und Tritium – auf mehr als 100 Mio. Kelvin aufgeheizt, wobei das resultierende Plasma mithilfe von Magnetfelder in der Schwebe gehalten wird. Bei solchen Temperaturen ist ein kleiner Anteil der Kerne schnell genug um durch Kollision zu verschmelzen.

Die H-B11-Reaktion kann so jedoch nicht gezündet werden, da die Temperaturen (bzw. die Kollisionsgeschwindigkeiten) dafür bei weitem nicht ausreichen. Es müssen völlig andere Verfahren genutzt werden, um die Kerne zu beschleunigen, z. B. sogenannte Polywell-Fusoren, in denen sie von elektrostatischen Feldern angezogen werden. Dies ist jedoch zur Zeit eher ein Nischen-Forschungsbereich, die meisten großen, staatlich unterstützten Fusionsexperimente nutzen Magneteinschluss und als Brennstoffe Deuterium und Tritium.

Aufgabe
Welche Energie wird bei der Reaktion

[math]!^2H \, + \, ^3H \longrightarrow \, ^4He + n[/math]

frei?

Atomgewichte: Deuterium H2: 2.0141 u, Tritium H3: 3.016 u, Helium 4: 4.0026 u, Neutron: 1.0087 u.

Lösung
Wieder hilft uns die Massenbilanz „Massen hinterher minus Massen vorher“:

[math]!\Delta M / \mathrm{u} = 4.0026 + 1.0087 – 3.016 – 2.0141 = -0.0188[/math]

woraus die freigesetzte Energie folgt:

[math]!\Delta W = 0.0188 \times 931.5 \, \mathrm{MeV} \approx 17.5 \, \mathrm{MeV}[/math]

der größte Anteil davon (ca. 14 MeV) geht in die kinetische Energie des freigesetzten Neutrons. Es muss daher im Mantel des Fusionsreaktors abgebremst werden, damit seine Energie in Form von Wärme extrahiert werden kann. Zusätzlich werden die Neutronen benötigt, um aus Lithium Tritium zu erbrüten, da letzteres aufgrund seiner Kurzlebigkeit natürlich kaum vorkommt.

Kernfusion ist ein äußerst komplizierte Technologie. Es müssen Wege gefunden werden, die Kerne mit sehr hohen Geschwindigkeiten kollidieren zu lassen. Die heutigen Fusionsexperimente verbrauchen daher immer noch mehr Energie als sie freisetzen. Mit ITER könnte sich dies jedoch bald ändern.

Einfacher ist es, Kernenergie auf umgekehrtem Wege freizusetzen: Durch Spaltung schwerer Kerne statt Verschmelzung leichter. Diese Energiequelle steht schon seit Mitte des 20. Jahrhunderts zu Verfügung, und es sind bereits Reaktoren der IV. Generation an der Startlinie. In diesem Mini-Lehrgang möchte daher schwerpunktmäßig die bereits großtechnisch umgesetzte Spaltung behandeln, im letzten Kapitel allerdings auch die Fusion.

Spaltung ist deutlich einfacher als Fusion, da bei ihr keine positiv geladenen Teilchen zur Kollision gebracht werden müssen, sondern es werden Neutronen genutzt, instabile Kerne zur Spaltung anzuregen. Neutronen dringen in Kerne ein, ohne abgestoßen zu werden. Wieso lassen sich dadurch Spaltungen auslösen?

Verschmilzt ein Neutron mit einem Kern, wird ein gewisser Energiebetrag freigesetzt, denn es wird von der Starken Kernkraft angezogen und zumindest vorrübergehend gebunden. Bei Kernen mit ungerader Massenzahl ist diese sogenannte Anlagerungsenergie besonders hoch, denn wenn das Neutron einen g/u-Kern vorfindet, kann es sich mit dem unverpartnerten Neutron magnetisch zusammenlagern (5. Term der Bethe-Weizsäcker-Formel) und dabei eine Spinenergie von 0.5 MeV freisetzen.

Die freigewordene Energie regt den Kern zu Formschwingungen an: Er oszilliert hin und her zwischen der Gestalt einer Zigarre und eines Tellers. Massive, instabile Kerne können hierdurch aus dem Gleichgewicht gebracht und in zwei (sehr selten in drei oder mehr) Bruchstücke gesprengt werden. Die Bruchstücke sind energetisch so hoch angeregt, dass sie fast augenblicklich einige neue Neutronen (sog. Spaltneutronen) freisetzen. Dies funktioniert bei Uran 233, Uran 235 und Plutonium 239. Um Uran 238 oder Thorium 232 zu spalten sind schnelle Neutronen nötig, da keine Spinenergie zur Verfügung steht, und die zur Spaltungsinitiierung benötigte Energie daher als kinetische Energie vom Neutron mitgebracht werden muss. Die Nuklide mit ungeraden Massenzahlen dagegen können auch von „thermischen“ Neutronen gespalten werden, d.h. von Neutronen, deren kinetische Energie der thermischen Energie der umgebenden Atome entspricht.

Definition:

• Kerne, die sowohl durch langsame (thermische) wie durch schnelle Neutronen gespalten werden können, nennen wir fissil. Bsp.: U233, U235, Pu239.
• Kerne, die durch schnelle oder langsame Neutronen gespalten werden können, nennen wir fissionabel (Anm.: Mir ist bisher nur das englische Wort „fissionable“ untergekommen, Übersetzung geraten). Die fissilen Kerne sind eine Untermenge der fissionablen, die alle Uranisotope und Transurane umfassen.
• Kerne, die durch Einfang eines Neutrons zu einem fissilen Kern transmutiert werden können, nennen wir fertil. Bsp.: Th232 (zu U233), U238 (zu Pu239).

Aufgabe
Ein Neutron spalte einen U235-Kern nach folgender Reaktionsgleichung in zwei Tochterkerne und zwei Spaltneutronen:

[math]!n \, + \, ^{235}U \longrightarrow \, ^{140}Xe \, + \, ^{94}Sr \, + \, 2n[/math]

wieviel Energie wird freigesetzt?
Atommassen: Neutron: 1.0087 u, U235: 235.0439 u, Xe140: 139.9216, Sr94: 93.9154

Lösung
Massenbilanz (ja, Einsteins Formel ist… universell!):

[math]!\Delta M / \mathrm{u} = 139.9216 \, + \, 93.9154 \, + \, 2 \times 1.0087 \, – \, 1.0087 \, – \, 235.0439 = -0,1982[/math]

Entsprechend einer Energie:

[math]!\Delta W = 0.1982 \times 931.5 \, \mathrm{MeV} = 184,6233 \, \mathrm{MeV}[/math]

Die beiden Tochterkerne sind meistens sehr instabil und zerfallen rasch weiter, wobei sie Betastrahlung (Elektronen oder Positronen), Neutrinos, Gammastrahlung, oder auch noch einige weitere Neutronen aussenden. Die Gesamtenergie pro Spaltung eines U233, U235 oder Pu239-Kerns liegt daher ziemlich genau bei

[math]!W_\mathrm{fiss} \approx 200 \, \mathrm{MeV}[/math]

Sie verteilt sich folgendermaßen:

• Kinetische Energie der Tochterkerne (Spaltprodukte): 170 MeV
• Kinetische Energie der Spaltneutronen: 5 MeV
• Prompte (d.h. bei der Spaltung entstehende) Gammastrahlung: 7 MeV
• Gammastrahlung der Spaltprodukte: 6 MeV
• Betastrahlung der Spaltprodukte: 6 MeV
• Neutrinos: 9 MeV
• Gesamt: 203 MeV

Die Neutrinos wechselwirken kaum mit Materie: Sie tragen ihre Energie daher aus dem Reaktor heraus, die 9 MeV gehen verloren. Dieser Verlust wird durch Neutroneneinfang-Reaktionen, die zusätzlich Energie freisetzen, ausgeglichen.

Aufgabe
Welche Geschwindigkeit haben Spaltprodukte bzw. Spaltneutronen?

Lösung
Die kinetische Energie pro Nukleon in den Spaltkernen beträgt ungefähr:

[math]!\epsilon_\mathrm{Nukleon} = \frac{170 \, \mathrm{MeV}}{233} \approx 0.73 \, \mathrm{MeV}[/math]

(Division durch 233 = 235 – 2 Spaltneutronen). Dies entspricht einer Geschwindigkeit:

[math]!v_\mathrm{Spaltprodukte} = \sqrt{\frac{2 \epsilon_\mathrm{Nukleon}}{1 \, \mathrm{u}}} \approx 12.000 \, \mathrm{km}/\mathrm{s}[/math]

Das sind etwa 4% der Lichtgeschwindigkeit!

Die 2 Spaltneutronen tragen je eine kinetische Energie von:

[math]!\epsilon_\mathrm{n} = \frac{5 \, \mathrm{MeV}}{2} = 2.5 \, \mathrm{MeV}[/math]

entsprechend der Geschwindigkeit (Neutronenmasse [math]M_\mathrm{n} = 1.0087 \, \mathrm{u}[/math]):

[math]!v_\mathrm{n} = \sqrt{\frac{2 \epsilon_\mathrm{n}}{m_\mathrm{n}}} \approx 30.000 \, \mathrm{km}/\mathrm{s}[/math]

Mit 10% der Lichtgeschwindigkeit nähern sich die Spaltneutronen bereits dem relativistischen Bereich (unsere Newton’sche Rechnung ist aber immer noch eine gute Näherung bei dieser Geschwindigkeit, der relativistische Faktor liegt bei [math]v^2/c^2 = 0.01[/math]).

Die Massenverteilung der Spaltprodukte für die drei fissilen Kerne (U233, U235, Pu239) zeigt dieses Diagramm, in dem der prozentuale Anteil der Spaltprodukte über dem Atomgewicht aufgetragen ist:

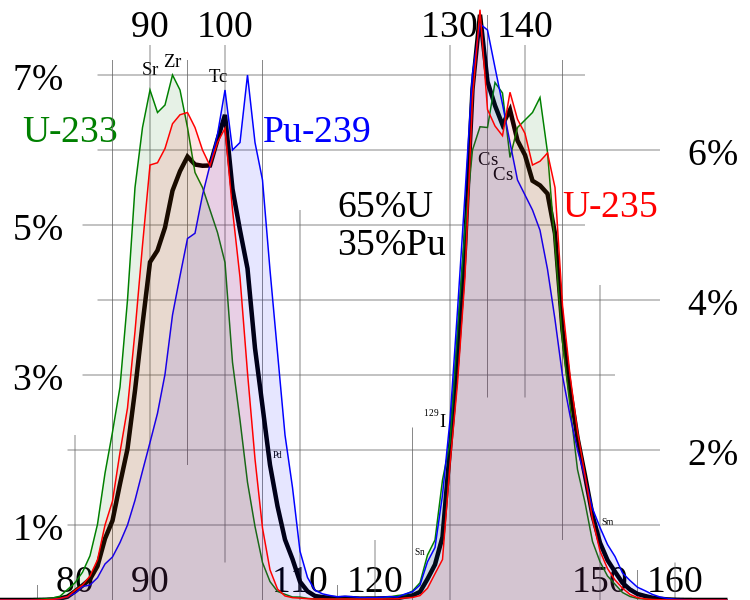
Es existieren ca. 60 primäre Spaltprodukte. Wie aus der Kamelhöckerform der Kurve hervorgeht, sind symmetrische Spaltungen (beide Tochterkerne gleich schwer) sehr selten.

Aufgabe
Welchen Energiegehalt hat 1 kg Fissilstoff (z. B. U235)?

Lösung

[math]!W(1 \, \mathrm{kg}) = 1 \, \mathrm{kg} \, \times \, \frac{200 \times 1.6 \times 10^{-13} \, \mathrm{J}}{235 \times 1.66 \times 10^{-27} \, \mathrm{kg}} \approx 80 \, \times \, 10^{12} \, \mathrm{J}[/math]

Ein Kilogramm Uran 238 (oder Uran 233 oder Plutonium 239) enthält 80 Millionen Megajoule Energie! Dies entspricht dem Energiegehalt von 2.2 Millionen Litern Benzin: rund 70 große Tanklastzüge!

Aufgabe
Wieviele U235-Kerne müssen in einem Großreaktor, der 3000 MW thermische Energie (entsprechend 1000 MW elektrische Energie bei Leichtwasserreaktor) umsetzt, pro Sekunde gespalten werden? Welcher Materialmasse entspricht dies?

Lösung
Zahl Spaltungen pro Sekunde = Leistung durch Energiefreisetzung pro Spaltereignis:

[math]!\dot{N} = \frac{3 \times 10^9 \, \mathrm{W}}{200 \, \mathrm{MeV}} \approx \frac{3 \times 10^9 \, \mathrm{J}/\mathrm{s}}{200 \times 1.6 \times 10^{-13} \, \mathrm{J}} \approx 9.4 \times 10^{19} \, \mathrm{s}^{-1}[/math]

Entsprechend einer pro Sekunde verbrauchten Masse an U235 von:

[math]!\dot{m_{235}} = 9.4 \times 10^{19} \, \times \, 235 \times 1.66 \times 10^{-27} \, \mathrm{kg} \, \mathrm{s}^{-1} \approx 36.7 \, \mu\mathrm{g} \, \mathrm{s}^{-1}[/math]

Pro Tag entspricht dies einem Verbrauch von 3.2 kg Uran. Zum Vergleich: Ein Kohlekraftwerk verbrennt pro Gigawatttag (elektrisch) 10.000 bis 20.000 Tonnen Kohle!

Kernbrennstoffe haben millionenmal höhere Energiedichten als chemische Brennstoffe!

Zuweilen ist zu lesen: Bei der Kernspaltung wird Masse in Energie verwandelt. Das stimmt aber auch bei allen anderen Energiewandlungsprozessen, die Einstein’sche Formel gilt universell. Entscheidend ist, aus welchem Feld bzw. welcher Wechselwirkung die Masse bzw. Energie stammt! Bei chemischen Prozessen handelt es sich um das elektrische Feld der Atomhülle, in dem nur wenige Elektronenvolt an Energie gespeichert sind. Bei Kernreaktionen wird dagegen millionenmal mehr Energie (und damit Masse) aus dem Feld der Starken Kernkraft freigesetzt. Bei Materie-Antimaterie-Zerstrahlung schließlich wird das Farbkraft-Feld im Inneren der Protonen und Neutronen, von dem das Kernkraft-Feld nur ein Randeffekt ist, aufgebrochen. Hierdurch wird die komplette Ruhemasse in Energie umgewandelt: 931.5 MeV pro atomare Masseneinheit, entsprechend ca. 90 Petajoule oder 2.8 Gigawattjahren pro Kilogramm Materie.

Aufgabe
Eine Person habe einen durchschnittlichen Primärenergieverbrauch von 10 kW (~nordamerikanisches Niveau). Welche Masse an 1. Kohle (Brennwert 30 MJ/kg), 2. Uran, 3. Deuterium+Lithium (aus Lithiumkern wird Tritiumkern erbrütet, dieser nimmt mit Deuterium an der Reaktion teil – Energiebilanz siehe Aufgabe weiter oben), 4. reinem Deuterium (4 MeV pro Kernreaktion), 5. Materie+Antimaterie benötigt sie im Laufe ihres Lebens (100 Jahre)?

Lösung
Insgesamt verbrauchte Energie:

[math]!W_\mathrm{Leben} = 100 \times 3.16 \, 10^7 \times 10^4 \, \mathrm{W} = 3.16 \times 10^{13} \, \mathrm{J} = 31.6 \, \mathrm{TJ}[/math]

Kohle
[math]!m_\mathrm{C} = \frac{W_\mathrm{Leben}}{30 \times 10^6 \, \mathrm{J}/\mathrm{kg}} \approx 1.05 \times 10^6 \, \mathrm{kg} \approx 1000 \, \mathrm{t}[/math]

Uran (oder anderes fissiles Schwermetall)
[math]!m_\mathrm{U} = \frac{W_\mathrm{Leben}}{200 \times 1.6 \, 10^{-13} \, \mathrm{J} / 235 \times 1.66 \times 10^{-27} \, \mathrm{kg}} \approx 0.37 \, \mathrm{kg}[/math]

In Worten: Einer 1000-Tonnen-Ladung Kohle (ca. 10 Güterwagen) entsprechen 370 Gramm Uran (Würfel mit 2.6 cm Kantenlänge)!!

D+Li Fusion
[math]!m_\mathrm{D+Li} = \frac{W_\mathrm{Leben}}{17.5 \times 1.6 \times 10^{-13} \, \mathrm{J} / (2 + 7) \times 1.66 \times 10^{-27} \, \mathrm{kg}} \approx 0.16 \, \mathrm{kg}[/math]

Die ca. 160 g Fusionsbrennstoff verteilen sich auf Deuterium und Lithium im Verhältnis 2 zu 7, d.h. 35.6 g Deuterium und 124.4 g Lithium.

Reine D-Fusion
[math]!m_\mathrm{D} = \frac{W_\mathrm{Leben}}{4 \times 1.6 \times 10^{-13} \, \mathrm{J} / 4 \times 1.66 \times 10^{-27} \, \mathrm{kg}} \approx 0.316 \, \mathrm{kg}[/math]

316 Gramm Deuterium sind in 9.6 Tonnen Wasser enthalten (33 g pro Tonne). Da auf der Erde rund [math]m_\mathrm{Hydrosphaere} \approx 1.3 \times 10^{18} \, \mathrm{t}[/math] Wasser vorhanden sind (97% davon in den Ozeanen), könnten 10 Milliarden Menschen rund 13.5 Millionen-mal ihren Lebensenergiebedarf (je 100 Jahre) daraus decken: Insgesamt 1.35 Milliarden Jahre lang!

Materie-Antimaterie-Zerstrahlung
[math]!m_\mathrm{Mat+Amat} = \frac{W_\mathrm{Leben}}{931.5 \times 1.6 \times 10^{-13} \, \mathrm{J} / 1.66 \times 10^{-27} \, \mathrm{kg}} \approx 0.34 \, \mathrm{g}[/math]

Rund ein Drittel Gramm, je zur Hälfte aufgeteilt auf Materie und Antimaterie, würde eine Person für ihr ganzes Leben benötigen!

Antimaterie kommt, soweit wir bislang wissen, in unserem Universum nur in kleinen Spuren vor. Sie kann jedoch von Teilchenbeschleunigern künstlich erzeugt werden, unter gewaltigem Energieaufwand: Ähnlich Wasserstoff bezüglich chemischer Verbrennung ist sie damit ein Energieträger und keine Energiequelle! Es wurde bereits vorgeschlagen, riesige Antimateriefabriken für Raumschiffantriebe auf Mond oder Merkur zur errichten und diese mit Solarenergie anzutreiben. Vielleicht werden in der Zukunft neuartige Verfahren zur Gewinnung von Antimaterie entdeckt, oder es gelingt, Materie direkt in Energie zu zerstrahlen (d.h. die Nukleonen aufzubrechen und die Farbkraft freizusetzen), ohne sie mit Antimaterie in Kontakt bringen zu müssen. Bezüglich letzterer Zukunftsspekulation ist allerdings zu beachten, dass bei Zerstörung eines Protons stets irgendwo eine positive Elementarladung erzeugt oder eine negative vernichtet werden muss, da die elektrische Ladung eine Erhaltungsgröße ist.

Vorerst steht von den genannten subatomaren Reaktionen nur die Spaltung schwerer Kerne (und, falls ITER die gewünschten Resultate erzielt, in näherer Zukunft auch die Verschmelzung leichter Kerne) zur Verfügung.

Wie erzeugt ein Kernreaktor kontrolliert Energie? Wie wir oben gesehen haben, setzt jede durch Einfang eines Neutrons induzierte Spaltung eines U233-, U235- oder Pu239-Kerns zwei bis drei (bzw. bei Spaltung durch schnelle Neutronen auch mehr) neue Neutronen frei. Diese können dazu dienen, weitere Spaltungen auszulösen, die wiederum Neutronen erzeugen, und immer so weiter: Es lässt sich eine neutronengeführte Kettenreaktion auslösen. Dazu ist es nötig, eine bestimmte Menge des fissilen Nuklids in einem gewissen Volumen zu konzentrieren: Denn die Kerne müssen nahe genug beieinander sein, damit die bei einer Spaltung freigesetzten Neutronen im Durchschnitt eine weitere Spaltung bewirken.

Im einfachsten Fall genügt eine zirka tennisballgroße Kugel aus U235, um eine Kettenreaktion aufrecht zu erhalten. Zur Energieproduktion wäre solch eine simple Anordnung aber ungeeignet. Kernreaktoren bestehen aus mehreren Komponenten:

1. Schwermetall mit hinreichend hoher Konzentration an fissilen Kernen (U233, U235 oder Pu239). Meistens sind auch fertile Kerne (Th232, U238) anwesend, die durch Neutroneneinfang teilweise in fissile umgewandelt werden.
2. Ein Moderator-Material mit niedriger Kernmasse, das die Spaltneutronen auf thermische Geschwindigkeiten abbremst: Denn in diesem Energiebereich ist die Wahrscheinlichkeit, Spaltungen auszulösen, besonders hoch. Meist wird Wasser oder Graphit genutzt. Es gibt auch schnelle Reaktoren ohne Moderator.
3. Ein Kühlmittel, das bei manchen Bauweisen zugleich als Moderator dient: Bei den meisten heutigen Leistungsreaktoren Wasser. Andere Typen benutzen Kohlendioxid oder Helium, bei schnellen Reaktoren werden flüssige Metalle (Natrium oder Blei/Wismuth-Eutektikum) oder auch Helium eingesetzt.
4. Ein Reflektor, der Neutronen, die aus dem Reaktor austreten, zurückwirft, damit sie für die Kettenreaktion zur Verfügung stehen.
5. Steuerungsmechanismen, mit denen die Kettenreaktion gestartet und angehalten und in ihrer Intensität (korrespondierend mit der thermischen Leistung) geregelt werden kann. Oft werden hierzu Stäbe aus neutronenabsorbierendem Material, die in den Reaktor geschoben oder herausgezogen werden können, eingesetzt. Andere Konzepte nutzen drehbare Zylinder außen um den Reaktor herum, die auf der einen Seite Neutronen absorbieren, auf der anderen reflektieren. Beschleunigergetriebene Systeme, die zur Aufrechterhaltung der Kettenreaktion ständig von außen mit Neutronen „gefüttert“ werden müssen, haben gar keine mechanischen Steuersysteme sondern werden über die Leistung des Beschleunigers geregelt.
6. Strukturmaterial, dass den Reaktor zusammenhält.

Die meisten heutigen Kernkraftwerke benutzen Leichtwasserreaktoren. Sie enthalten Brennstäbe aus Uranoxid, dessen Anteil an U235 auf einige Prozent angereichert wurde (in der Natur liegt er bei 0.7%, beinahe der gesamte Rest ist U238). Ein größere Anzahl von Brennstäben wird zu einem Brennelement mit rechteckigem Querschnitt zusammengefasst. Als Kühlmittel und Moderator dient Wasser. Beim Siedewasserreaktor verdampft es direkt im Reaktor selbst und treibt den Turbogenerator, es existiert nur ein Kühlkreislauf. Beim Druckwasserreaktor steht der Primärkreislauf, der den Reaktor kühlt, unter so hohem Druck dass das Wasser nicht verdampft, dies geschieht erst im Wärmetauscher, in dem der Sekundär- oder Turbinenkreislauf erhitzt wird. Nachdem er über die Turbinenschaufeln geströmt ist, kondensiert der Dampf wieder, wozu in Abwesenheit größerer Wassermengen (Fluss, See, Meer) oft Kühltürme als Wärmesenke eingesetzt werden.

Andere wichtige Reaktorbauarten, die in Zukunft an Bedeutung gewinnen werden, sind der Hochtemperaturreaktor, der als Moderator Graphit und zur Kühlung Helium oder Kohlendioxid nutzt, der Schnelle Brüter, der mit flüssigem Metall gekühlt wird und es durch seine gute Neutronenökonomie ermöglicht, fertiles U238 fast komplett in fissiles Pu239 umzuwandeln und so als ergiebige Energiequelle zu nutzen, sowie der Flüssigsalzreaktor, der überhaupt keine Brennstäbe hat sondern ähnlich einem chemischen Reaktor fissile und fertile Stoffe in flüssiger Form – gelöst in geschmolzenem Salz – durch die Reaktionszone pumpt.

Die Konstruktionsprinzipien der unterschiedlichen Reaktortypen sollen in späteren Kapiteln genauer erörtert werden. Im nächsten Teil werde ich den Mechanismus der Kettenreaktion darstellen und den zu seiner Beschreibung nötigen mathematischen Apparat entwickeln. Stay tuned!