Kernenergie – das Tor zum Weltraum

Alle Lebewesen auf der Erde mit Ausnahme des Menschen sind in ihrer Handlungsfähigkeit durch die eigene Körperkraft begrenzt: Sie können ihre Umwelt nur in geringem Maße verändern und wachsen daher in eine bestimmte ökologische Nische hinein, die sie nicht verlassen können. Menschen aber vermögen Dank Vernunft und wissenschaftlicher Kreativität ihre Lebenswelt komplett umzugestalten, indem sie mächtige Technologien erschaffen, durch die ihre Fähigkeiten um viele Größenordnungen gesteigert werden. Wir haben sogar die Fähigkeit entwickelt, unseren Planeten zu verlassen und in den Kosmos vorzudringen: Solcherart sind wir nicht nur nicht mehr an eine bestimmte ökologische Nische gebunden, wir lernen gerade sogar, Orte außerhalb der Erde als Lebensumwelt zu erschließen. Dies könnte darauf hindeuten, dass wir die erste Spezies auf der Erde sind, die nicht aussterben muß, sondern Millionen, vielleicht sogar Milliarden von Jahren lang fortzudauern vermag.

Bisher sind unsere bemannten Raumschiffe allerdings noch recht klein und reichen auch nicht sehr weit in den Kosmos hinein, denn die benötigten riesigen Energiemengen bringen chemische Antriebe rasch an ihre Grenzen. Raumflugkörper auf interplanetaren Bahnen müssen beträchtliche Geschwindigkeitsdifferenzen überwinden – typischerweise einige 10 Kilometer pro Sekunde. Die enorme Energiedichte der Atomkerne regt zu visionären Ideen an: Kann man Kernreaktionen nutzen, um ein Raumschiff anzutreiben? Man dachte schon bald nach der Konstruktion des ersten Reaktors (1942: Chicago Pile 1) darüber nach, ein nukleares Raumschiff zu entwickeln. Wie kann das funktionieren?

Es gibt viele Arten, sich die Mathematik und Mechanik des Raumfluges klarzumachen. Ich möchte hier eine wählen, die den Unterschied zwischen den drei wichtigsten Raketentypen – chemisch, elektrisch und nuklear – am besten verdeutlicht. Ich gehe dabei von dem Ereignis der Energiefreisetzung aus. Da es am Anfang des Antriebsprozesses steht, nenne ich es Elementarereignis: Im Fall der chemischen Rakete das Knüpfen oder Aufbrechen einer chemischen Bindung unter Energiefreisetzung, im Fall der nuklearen das Spalten eines Kerns in einige Bruchstücke (meist zwei Tochterkerne und mehrere Neutronen) oder das Verschmelzen zweier Kerne. Bei der chemischen Reaktion wird größenordnungsmäßig 1 eV pro AMU (Atomic Mass Unit – ca. Masse eines Nukleons) frei, bei nuklearen 1MeV pro AMU: Eine Million mal mehr!

Die freigesetzte Energieportion [math]\Delta W[/math] muss nun dazu genutzt werden, Reaktionsmasse aus der Raketendüse auszustoßen – denn eine andere Möglichkeit, zu beschleunigen, gibt es im Weltraum nicht, da man sich ja nirgends abstoßen kann.

Es soll die Massenportion [math]\Delta m[/math] beschleunigt werden. Nimmt sie die gesamte Energiemenge auf, so erreicht sie die Ausstoßgeschwindigkeit

[math]!v_0 = \sqrt{\frac{2 \Delta W}{\Delta m}}[/math]

mit der sie hinten aus dem Triebwerk ausgeworfen wird. Die Rakete wird dank Impulserhaltungssatz in die Gegenrichtung beschleunigt:

[math]!M_\mathrm{rak} \times \Delta v = \Delta m \times v_0[/math]

dabei ist [math]M_\mathrm{rak} = M_\mathrm{rak \, 0} – \Delta m[/math] die Masse der Rakete nach dem Materieausstoß, [math]\Delta v[/math] der Betrag, um den sich ihre Geschwindigkeit ändert:

[math]!\Delta v = \frac{\Delta m \times v_0}{M_\mathrm{rak}}[/math].

Entsprechend ändert sich ihr Impuls um:

[math]!\Delta I = \Delta v \times M_\mathrm{rak} = \Delta m \times v_0[/math].

Um zu wissen, wie effizient ein Triebwerk arbeitet, möchte man quantifizieren, wie gut es Reaktionsmasse in Impulszuwachs umwandelt – wie effizient die ausgestoßene Materie genutzt wird. Die leistet die Größe spezifischer Impuls:

[math]!I_\mathrm{sp} = \frac{\Delta I}{\Delta m \, g} = \sqrt{\frac{2 \Delta W}{\Delta m}} \, \times \, \frac{1}{g} = \frac{v_0}{g}[/math]

Hierbei ist [math]g \approx 9.81 \, \mathrm{m} \mathrm{s}^{-2}[/math] die Erdbeschleunigung. Auf den ersten Blick scheint sie nur ein konstanter Skalierungsfaktor zu sein. Sie mit in den spezifischen Impuls hineinzuziehen hat jedoch interessante Vorteile, wie wir nachher sehen werden. Der spezifische Impuls hat die Einheit Sekunde.

Zunächst möchten wir natürlich wissen, um welchen Betrag [math]\Delta v_\mathrm{e}[/math] die Rakete insgesamt ihre Geschwindigkeit ändern kann, wenn sie die gesamte Reaktionsmasse in ihren Tanks aufbraucht. Hierzu müssen wir von kleinen, aber diskreten Größen [math]\Delta m[/math] zu infinitesimalen [math]\mathrm{d}m[/math] übergehen und integrieren:

[math]!\Delta v_\mathrm{e} = \int_0^T \frac{\mathrm{d}I}{M(t)} = I_\mathrm{sp} g \, \times \, \int_0^T \frac{\mathrm{d}M}{M} = I_\mathrm{sp} g \, \times \, \ln{\left( \frac{M_0}{M_\mathrm{d}} \right)}[/math]

wobei [math]M_0[/math] die Masse der betankten Rakete vor Zündung der Triebwerke ist, und [math]M_\mathrm{d}[/math] die der „trockenen“ Rakete mit leeren Tanks nach Ablauf der Brenndauer [math]T[/math]. Diese berühmte Formel nennt man nach ihrem Entdecker Tsiolkowski’sche Raketenformel.

Das Massenverhältnis [math]R = \frac{M_0}{M_\mathrm{d}}[/math] kann auch anders aufgeschlüsselt werden:

[math]!R = \frac{M_0}{M_\mathrm{d}} = \frac{M_\mathrm{d} + M_\mathrm{p}}{M_\mathrm{d}} = 1 + \frac{M_\mathrm{p}}{M_\mathrm{d}}[/math]

wobei [math]M_\mathrm{p}[/math] die gesamte in den Tanks enthaltene Rückstoßmasse ist („Propellant“).

Wenn ein Raketensystem einen hohen spezifischen Impuls hat, kann es mit einer geringen Menge an Rückstoßmasse eine hohe Geschwindigkeitsänderung erzeugen. Dies bedeutet jedoch nicht, dass jede Rakete mit hohem [math]I_\mathrm{sp}[/math] auch eine große Schubkraft entwickelt! Im Gegenteil: elektrische Systeme haben viel höhere spezifische Impulse als chemische, und daher eine deutlich höhere Endgeschwindigkeit, aber ihre Schubkräfte sind sehr gering, da sie nur kleine Massenmengen ausstoßen. Sie können keine raschen Bahntransfers durchführen (und verlieren deshalb viel Energie durch Gravitationsbremsung), und sind auch nicht für Bodenstarts geeignet, da sie nicht ihr eigenes Gewicht im Erdschwerefeld heben können.

Die Schubkraft berechnet sich aus der Formel

[math]!F = \dot{M} \times v_0 = \dot{M} \times I_\mathrm{sp} \times g[/math]

wobei [math]\dot{M}[/math] die Massendurchflussrate in Kilogramm pro Sekunde ist. Wenn sie extrem gering ist wie bei elektrischen Triebwerken, dann entsteht trotz hoher Ausstoßgeschwindigkeit (bzw. hohem spez. Impuls) nur eine geringe Schubkraft. Nun sehen wir auch, warum im Nenner von [math]I_\mathrm{sp} = F / (\dot{M} \, g)[/math] die Erdbeschleunigung auftaucht: Multipliziert man den derartig definierten spezifischen Impuls mit der Massendurchflussrate, erhält man sofort die Masse, die der Antrieb im Erdschwerefeld zum Schweben bringt. Ist die Gesamtmasse der betankten Rakete geringer, kann sie vom Boden aus starten, ansonsten nicht.

Die heutzutage gebräuchlichen Raketen lassen sich in zwei Klassen einteilen:

• Schubstark, mit geringem spezifischem Impuls (< 500 s): Chemische Triebwerke.
• Schubschwach, mit hohem spezifischem Impuls (bis 10.000 s): Elektrische Triebwerke (auch genannt Ionen- oder Plasmatriebwerke).

Was müsste gegeben sein, damit beides zugleich – hoher Schub und hoher spezifischer Impuls – erreicht werden kann?

Zur Erzeugung einer bestimmten Schubkraft [math]F[/math] muss eine Anzahl [math]N[/math] an Elementarereignissen – Freisetzung einer Energiemenge und Beschleunigung einer Massenportion durch diese Energie – pro Zeiteinheit stattfinden:

[math]!N = \frac{F}{\Delta I} = \frac{F}{\sqrt{2 \, \Delta W \, \Delta M}}[/math]

Da jedes Elementarereignis die Energiemenge [math]\Delta W[/math] umsetzt, entspricht dies einer Leistung von:

[math]!P = \Delta W \times N = F \, \times \, \sqrt{\frac{\Delta W}{2 \, \Delta M}} = \frac{1}{2} \, \times \, I_\mathrm{sp} \, g \, F[/math]

Die Leistung eines Raketenmotors ist dem Produkt von Schubkraft und spezifischem Impuls proportional. Wollte man ein Triebwerk betreiben, dass eine Schubkraft von 12 MN (entsprechend einem großen chemischen Triebwerk wie den Feststoffboostern des Space Shuttles) bei einem spezifischen Impuls von 5000 s erzeugt, müsste eine Leistung von 294 GW freigesetzt werden – mehr als die Hälfte des Primärverbrauchs von ganz Deutschland!

Die Feststoffbooster wiesen nur einen spezifischen Impuls von 242 s auf. Sie hatten daher eine Leistung von jeweils 14 GW.

Eine Kombination von hohem spezifischem Impuls und hoher Schubkraft ist wünschenswert, um rasche interplanetare Missionen mit hoher Nutzlast ohne „Stufenwildwuchs“ durchführen zu können. Um mit chemischen Raketen größere Geschwindigkeitsänderungen [math]\Delta v[/math] erzielen zu können, ist man auf Mehrstufenraketen angewiesen, da das Massenverhältnis sich nicht beliebig steigern lässt – die Tanks würden oberhalb einer bestimmten Größe unter ihrem eigenen Gewicht bersten. Für einen Flug vom Erdboden in eine niedrige Umlaufbahn (LEO: Low Earth Orbit, eine Kreisbahn wenige hundert km über der Erdoberfläche) ist eine Geschwindigkeit von 10 km pro Sekunde nötig, 8 km pro Sekunde reine Umkreisungsgeschwindigkeit und 2 km pro Sekunde zur Überwindung von Luftreibung und Gravitation:

[math]!10^4 \, \mathrm{m} \mathrm{s}^{-1} = 450 \, \mathrm{s} \, \times 9.81 \, \mathrm{m} \mathrm{s}^{-2} \, \ln{\left( \frac{M_0}{M_\mathrm{d}} \right)}[/math]

Ein spezifischer Impuls von 450 s lässt sich mit den stärksten chemischen Triebwerken auf Wasserstoff-Sauerstoff-Basis erreichen. Aber selbst hiermit wäre ein Massenverhältnis von 9.23 nötig, wesentlich mehr als realisierbar ist. Es lassen sich in der Praxis kaum Raketen mit [math]R \textgreater 4[/math] bauen. Daher benutzt man Mehrstufensysteme, die das Massenverhätnis künstlich steigern, indem leergebrannte Tanks unterwegs abgeworfen werden. Und selbst mit diesem Trick ist es kaum machbar, wesentlich mehr als 100 Tonnen auf einmal in die Umlaufbahn zu bringen – die Saturn V vermochte 120 t in eine niedrige Umlaufbahn zu transportieren, das Shuttle schaffte nur 24.5 t. Große Nutzlasten im Bereich von 1000 t, wie sie für bemannte interplanetare Missionen benötigt würden, müsste man heutzutage mit vielen Raketenstarts nacheinander hinauf schaffen. Und das interplanetare Schiff selbst bestünde wiederum vor allem aus Treibstofftanks, die unterwegs nacheinander abgeworfen werden würden.

Daher stellt sich offensichtlich die Frage, ob man nicht wesentlich effizientere Raketen bauen kann, die dank großem spezifischem Impuls (im Bereich von mehreren 1000 s wie bei Ionenantrieben) und großer Schubkraft (im Bereich von 10 MN wie bei chemischen Raketen) hohe Nutzlasten ins LEO oder sogar bis zu anderen Himmelskörpern in unserem Sonnensystem und wieder zurück zu bringen vermögen, ohne das komplizierte Mehrfachstarts und Mehrstufenkonstruktionen nötig sind. Ein hinreichend leistungsstarkes Triebwerk würde es sogar erlauben, interplanetare Flüge wesentlich rascher durchzuführen, als es auf den momentan genutzten Hohmann-Bahnen möglich ist, mit Transitzeiten von Wochen statt Monaten, was die psychologische und physiologische Belastung für die Astronauten stark reduzieren würde.

Hier kommen nukleare Antriebe ins Spiel. Die hohen Energiedichten von Kernbrennstoffen lassen prinzipiell fast beliebig hohe Leistungen zu. In der Praxis gibt es dabei natürlich einige Knifflichkeiten zu überwinden. Wie lassen sich Kernreaktionen nutzen, um Schub zu erzeugen? Zuerst kann man auf den Gedanken kommen, genau wie bei den chemischen Raketen vorzugehen, und die Reaktionsprodukte selbst hinten auszustoßen. Bei Kernspaltungen steckt die Reaktionsenergie im Wesentlichen in der kinetischen Energie der Fragmente mit einer Dichte von ca. 1 MeV / AMU, entsprechend einer Geschwindigkeit von über 10.000 Kilometern pro Sekunde oder einem spezifischen Impuls von 1000.000 Sekunden.

Schwierig dürfte es natürlich sein, die Spaltprodukte überhaupt aus einem Reaktor herauszubekommen, da sie ja normalerweise im Spaltstoff gefangen bleiben. Dennoch wurden solche Raketen bereits vorgeschlagen: Man überlegt, das fissile Material auf dünne Fäden aufzubringen, die mit hohem Tempo durch die Reaktionszone gezogen werden, oder aber es als Staub in einem elektrischen Feld zum Schweben zu bringen. Ein Magnetfeld soll die Spaltprodukte herauslenken.

Dokumentation

• Chapline et al. (1989): Fission Fragment Rockets – a new Frontier
• Next Big Future: Fission Fragment Rocket Engine Thrust Velocity at 1.7% of light speed

Den Nachteil solcher (bislang hypothetischen) Konstruktionen sieht man, wenn man den zu erwartenden Schub pro Leistung ausrechnet:

[math]!F = \frac{2 \, P}{g \, I_\mathrm{sp}}[/math]

Für nur ein einziges Newton Schub bräuchte man 5 MW Leistung! Selbst ein Großreaktor mit 3 GWth würde nur eine Schubkraft von 600 N erfahren, wenn man seine Spaltprodukte dazu bringen könnte, alle in eine bestimmte Richtung zu fliegen, was gerade mal dazu ausreichen würde, eine Masse von 60 kg im Erdschwerefeld zum Schweben zu bringen. Man sieht, dass eine solche Rakete eher Eigenschaften eines Ionenantriebs hätte: Hoher spezifischer Impuls, aber kleiner Schub.

Wie können wir den Schub steigern? Natürlich durch senken des spezifischen Impulses. Man kann sich diesen Mechanismus wie die Gangschaltung bei einem Auto oder Fahrrad denken: Die Antriebsleistung bleibt konstant, aber durch Ändern der Übersetzung lässt sich Schubkraft gegen Ausstoßgeschwindigkeit tauschen.

Der Impulsübertrag pro Elementarereignis

[math]!\Delta I = \sqrt{2 \Delta W \Delta m}[/math]

lässt sich durch Erhöhung von [math]\Delta m[/math], der Massenportion, die von jedem Ereignis mit Energie gespeist wird, vergrößern – bei entsprechend geringerer Ausstoßgeschwindigkeit bzw. spezifischem Impuls. Die von den Kernreaktionen freigesetzte Energie muss hierzu in eine größere Rückstoßmasse geleitet werden, und diese beschleunigen. Man verlässt dabei die Vorgabe der chemischen Rakete, dass Energieträger und Rückstoßmasse identisch sind – hier werden sie getrennt: Energie liefert der Reaktor und überträgt sie auf das zu beschleunigende Medium, das aber selbst bei der Energieerzeugung nicht mitwirkt.

Am einfachsten lässt sich dies realisieren, indem man quasi einen gasgekühlten Hochtemperaturreaktor mit offenem Kühlkreislauf baut: Ein Arbeitsgas wird durch einen Reaktor hindurch geleitet, dadurch erhitzt und aus einer Düse ausgestoßen. Dies war die Idee hinter dem Nuklearraketenprogramm der US Air Force und später der NASA von den 1940ern bis in die 70er, das im Rahmen der Projekte Rover und NERVA zum ersten Mal demonstrierte, dass Kernreaktoren als Raketenantrieb sehr wohl geeignet sind.

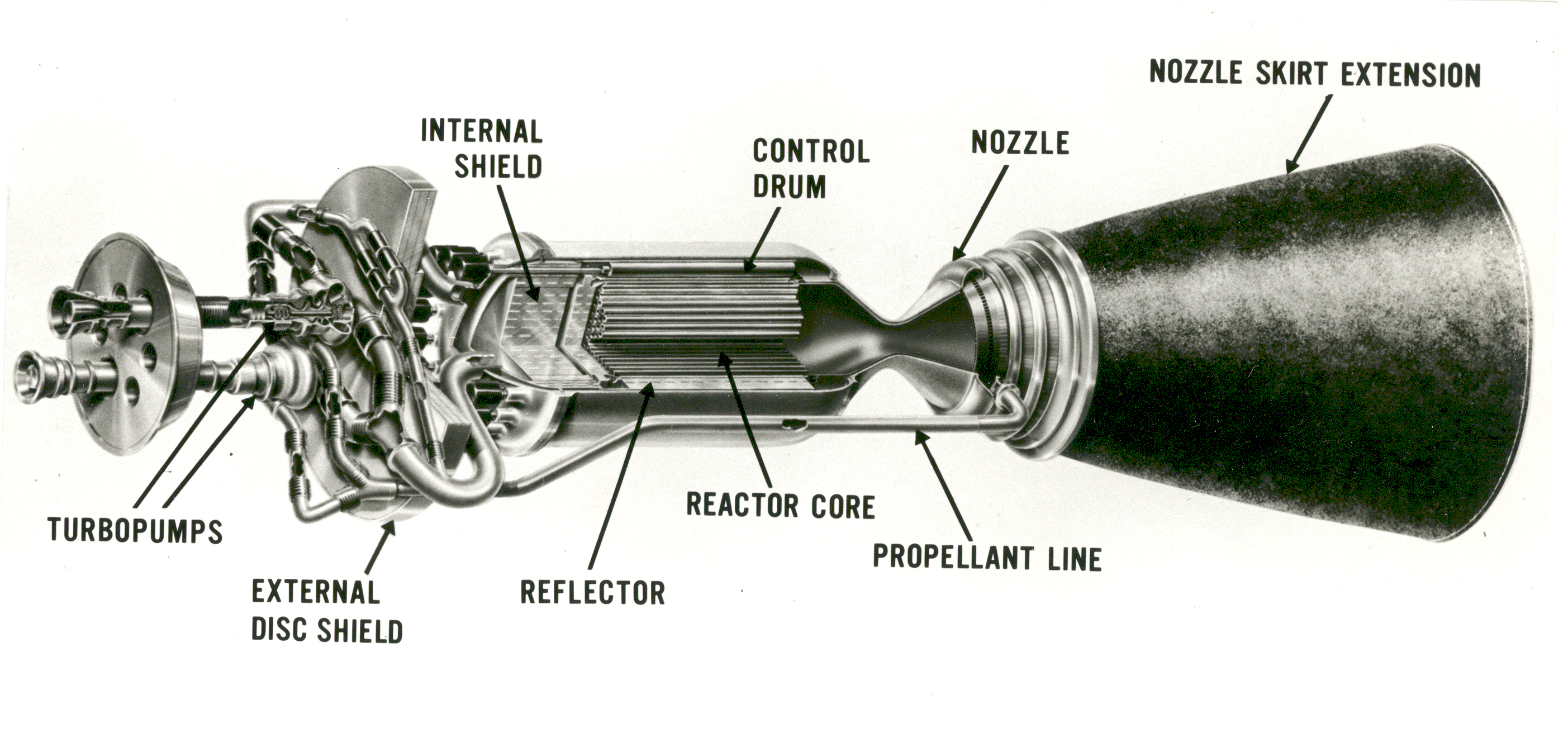
Als Arbeitsgas wählte man Wasserstoff – dessen niedriges Atom- bzw. Molekülgewicht (1 bzw. 2 AMU) erlaubt besonders hohe Ausstoßgeschwindigkeiten. Wird das Gas auf eine Temperatur [math]T[/math] (in Kelvin) erhitzt, gilt näherungsweise:

[math]!v_0 \approx \sqrt{\frac{T}{m_\mathrm{M} / 1 \, \mathrm{AMU}}} \, \times \, Z \times 129[/math]

mit dem Molekulargewicht des Arbeitsgases [math]m_\mathrm{M}[/math] und dem designspezifischen Wärme-Druck-Faktor [math]Z[/math], der zwischen 1.4 und 2.4 liegt.

Das bedeutet, dass bei dieser Art von Rakete die Chemie bzw. Festkörperphysik bis zu gewissem Grad die Kernenergie ausbremst, da der Reaktor eine werkstofflich vorgegebene Temperaturobergrenze nicht überschreiten darf, damit er nicht schmilzt.

Bei den Experimenten der NASA arbeiteten die Reaktoren im Bereich von ca. 2500 K – dies ergab bei Nutzung von molekularem Wasserstoff spezifische Impulse, die die von chemischen Raketen ca. um das Doppelte übertrafen: 800… 1000 Sekunden.

Bisher sind nuklearthermische Triebwerke (NTR – Nuclear Thermal Rocket) noch nicht geflogen: Sie wurden nur am Boden getestet, dies allerdings mit beträchtlichem Erfolg. Obwohl sie auf den ersten Blick wie ein Kompromiss zwischen chemischem und elektrischem Antrieb wirken – spezifischer Impuls doppelt so groß wie bei chemischen Raketen, Schub deutlich größer als bei elektrischen (bis 890 kN), aber noch nicht ausreichend zum Bodenstart – haben sie viel Potential. Eine bemannte Marsmission ließe sich mit ihnen schneller und mit größerer Nutzlast durchführen als mit chemischen Antrieben. Und mit einigen technischen Weiterentwicklungen ließen sich die Fähigkeiten der NTR noch deutlich verbessern. Nähme man statt Reaktorbrennstäben kugelförmige Brennstoffpartikel, die sich in einer rotierenden Trommel mit Öffnungen befinden, durch die das Wasserstoffgas strömt, ließen sich Temperatur und Leistung so stark erhöhen, dass spezifische Impulse bis zu 1050 Sekunden und Bodenstarts möglich wären. Eine andere interessante Option, die vorgeschlagen wurde, ist die LANTR: Liquid Oxygen assisted NTR. Bei ihr handelt es sich um ein Kombisystem aus nuklearem und chemischem Antrieb. Um den Schub zu erhöhen (und im Gegenzug den spezifischen Impuls zu senken), kann flüssiger Sauerstoff hinter dem Reaktor in die Düse eingespritzt werden, wodurch der Effekt eines chemischen Nachbrenners entsteht. So erhält man eine Rakete mit zwei „Gängen“: Niedriger Schub, hoher spezifischer Impuls (800… 1000 Sekunden, reiner NTR-Modus), höherer Schub, niedriger spezifischer Impuls (ca. 600 Sekunden, LOX-Nachbrenner).

Dokumentation

• Borowski et al. (2012): Nuclear Thermal Rocket (NTR) Propulsion: A Proven Game-Changing Technology for Future Human Exploration Missions
• Lawrence et al. (2005): Nuclear Thermal Rocket Propulsion Systems, IAA White Paper
• Borowski et al. (1997): „2001: A Space Odyssey“ Revisited — The Feasibility of 24 Hour Commuter Flights to the Moon Using NTR Propulsion with LUNOX Afterburners – ein Projekt zur Industrialisierung des Mondes mithilfe von LANTR. Der Sauerstoff soll hierbei auf dem Mond selbst aus Gesteinen gewonnen werden!
• Next Big Future: Nuclear DC-X – einstufige(!) LANTR-Trägerrakete, die 100 t in eine niedrige Umlaufbahn bringt.

Obwohl NTR oder auch LANTR einen deutlichen Fortschritt gegenüber chemischen Raketen darstellen, kann man bis zu gewissem Grad den Eindruck bekommen, dass die Kernenergie hier unnötig in Fesseln gelegt wird, bedingt durch die Notwendigkeit, den Reaktorkern nicht zu überhitzen. Eine offensichtliche Lösung besteht darin, überhaupt keinen festen Reaktorkern zu verwenden. Flüssige Kerne wurden vorgeschlagen, sind aber vermutlich als Raketenantrieb nicht so geeignet: Viele Wissenschaftler streben an, noch einen oder gleich zwei Aggregatzustände höher zu gehen, und gas- oder plasmaförmige Spaltstoffe in einem sogenannten Gaskernreaktor bei Temperaturen von bis zu mehreren 10.000 K zu nutzen. Solche Maschinen befinden sich bislang erst im experimentellen Stadium, könnten uns aber im Erfolgsfall unserem Ziel (großer spezifischer Impuls plus hohe Schubkraft) einen großen Schritt näher bringen.

Gaskernreaktoren ließen sich auf zweierlei Arten bauen: Offen und geschlossen. Der offene Reaktor schließt das Spaltstoffplasma nirgendwo ein, es wird vielmehr hydrodynamisch – in manchen Entwürfen auch durch Magnetfelder oder Rotation – in der Schwebe gehalten und dabei vom Arbeitsgas Wasserstoff um- und durchströmt. Dieses Vorgehen erlaubt sehr hohe Arbeitstemperaturen, und spezifische Impulse bis hin zu 7000 Sekunden. Es stellt aber eine große Herausforderung dar, einen übermäßigen Verlust von Spaltstoff durch die Düse, der die Effizienz herabsetzen oder sogar die Kettenreaktion zum Erliegen brächte, zu vermeiden. Der geschlossene Gaskernreaktor sperrt das Uranplasma in Quarzglasgefäße – sogenannte nukleare Glühbirnen – ein, wobei es durch ein Puffergas (Neon) von den Wänden ferngehalten wird. Der Wasserstoff strömt außen um den Kolben herum und wird durch Ultraviolettabstrahlung des Plasmas aufgeheizt. Die Arbeitstemperatur von ca. 10.000 K erlaubt spezifische Impulse bis zu 3000 Sekunden.

Dokumentation

• Jerry Grey (1959): Gaseous-core nuclear rockets – ein sehr frühes, spekulatives Paper zu dem Thema.
• Robert G. Ragsdale (1971): High-Specific-Impulse Gas-Core Reactors
• The Liberty Ship – Entwurf einer gewaltigen einstufigen Trägerrakete, die von 7 nuklearen Glühbirnen angetrieben wird, 1000 t ins Orbit transportieren und anschließend kontrolliert (d.h. auf ihrem Abgasstrahl schwebend) landen kann.

Das klingt alles schon ganz nett! Aber wir haben noch viel weiter gesteckte Pläne. Anstatt 1000 Tonnen nur von der Erdoberfläche ins LEO zu verfrachten, möchten wir mit 1000 t Nutzlast starten, zum Saturnmond Enceladus fliegen und wieder zurück – alles mit nur einer einzigen Raketenstufe! Das ist mit vorhandener Technologie möglich: Sofern wir unsere bisherigen Vorstellungen, wie eine Rakete aufgebaut sein sollte, über Bord werfen, und, um es auf gut Englisch zu sagen, a walk on the wild side riskieren!

Als die Sowjetunion in den 1950ern einen Raumfahrterfolg nach dem anderen erzielte, machten in den Vereinigten Staaten Wernher von Braun und sein Team sich daran, große chemische Raketen zu entwickeln, um den weltpolitischen Gegner zu überholen und Menschen bis auf den Mond zu bringen, was ihnen auch gelang. Einige Wissenschaftler, unter ihnen der bekannte Freeman Dyson, dachten weiter: Der Wettlauf zwischen Ost und West mit chemischen Raketen schien ihnen eine Art Ochsenkarrenrennen zu sein. Warum nicht vom Ochsenkarren ins Rennauto umsteigen und den Sowjets davonrasen?

Das Rennauto sollte in diesem Fall eine nukleare Rakete sein. Aber keine, der durch den Schmelzpunkt ihres Reaktors Fesseln angelegt sind. Wir erinnern uns, dass zur Realisierung eines Antriebs mit hoher Schubkraft und hohem spezifischem Impuls sehr hohe Leistungen im Bereich des Energieverbrauchs eines ganzen Landes nötig sind. Solche Leistungsdichten kann man nicht in Form einer kontrollierten Reaktion in einer normalen Brennkammer einsperren ohne dass die ganze Maschine verdampft. Wenn man die enorme Energiedichte der Kerne wirklich ausnutzen will, darf die Energiefreisetzung nicht durch die Stabilität umgebender Materialien begrenzt werden: Sie muss außerhalb der Rakete erfolgen, und zwar in Form einer prompt-überkritischen Kettenreaktion – mit anderen Worten, durch Nuklearexplosionen, wie Kernwaffen sie hervorrufen.

Wie können Bomben ein Raumschiff antreiben?

An für sich ganz einfach: Man lässt sie nacheinander, etwa mit einem Abstand von einer Sekunde, hinter dem Schiff explodieren, das entstehende Plasma prallt gegen eine große Absorberplatte, die durch Stoßdämpfer mit dem Schiff verbunden ist, und treibt dieses Stoß für Stoß vorwärts. Da das Plattenmaterial jeweils nur sehr kurz (Millisekunden) mit dem Plasma in Kontakt kommt, erfährt es nur geringe Ablation, ähnlich wie das Innere eines Kolbens in einem Verbrennungsmotor nicht verdampft, obwohl die Temperatur der Verbrennungsgase kurzzeitig den Siedepunkt des Metalls überschreitet.

Dieses Konzept nannte man Orion-Antrieb, oder External Pulsed Plasma Propulsion.

Wir wollen die Leistungsfähigkeit eines Orionschiffs größenordnungsmäßig abschätzen.

Eine der Kernbomben habe die Explosionsenergie [math]W_\mathrm{B}[/math]. Vereinfachend nehmen wir an, dass sie komplett in kinetische Energie des Plasmas umgewandelt wird, das dadurch mit der Geschwindigkeit

[math]!v_\mathrm{P} = \sqrt{\frac{2 W_\mathrm{B}}{m_\mathrm{P}}}[/math]

kugelförmig expandiert, wobei [math]m_\mathrm{P}[/math] seine Masse – d.h. die Masse der Bombe – ist.

Die Explosion erfolgt in einem Abstand [math]d[/math] von einer runden Prallplatte mit Radius [math]r[/math]. Dann trifft der Anteil

[math]!\bar{m}_\mathrm{P} = m_\mathrm{P} \times f = m_\mathrm{P} \, \times \, \frac{1}{2} \left(1 – \cos{\theta}\right)[/math]

des Plasmas die Platte, wobei [math]\theta = \arctan{(r/d)}[/math] der Winkel ist, den der Radius der Prallplatte am Explosionsort aufspannt. Dabei kommt es zu einem Impulsübertrag auf die Rakete

[math]!\Delta I = \Delta v \times m_\mathrm{Rak} = 2 \times \bar{m}_\mathrm{P} \times v_\mathrm{P} = m_\mathrm{P} \, \times \, \left(1 – \cos{\theta}\right) \, \times \, v_\mathrm{P}[/math]

wobei ein völlig elastischer Stoß angenommen (Faktor 2) und vernachlässigt wurde, dass das Plasma nicht überall senkrecht auftrifft. Es folgt der spezifische Impuls:

[math]!I_\mathrm{sp} = \frac{\Delta I}{m_\mathrm{P} g} = \sqrt{\frac{2 W_\mathrm{B}}{m_\mathrm{P}}} \, \times \, \frac{1 – \cos{\theta}}{g}[/math]

Man sieht, dass der spezifische Impuls zum einen mit dem scheinbaren Winkeldurchmesser [math]\theta[/math] der Prallplatte – d.h. bei fixem Explosionsabstand mit dem Plattendurchmesser – zum anderen mit der spezifischen Energiedichte der Bomben [math]W_\mathrm{B}/m_\mathrm{P} = \chi[/math] wächst.

Damit nicht ein Großteil der Explosionsenergie verloren geht, soll es sich bei den Bomben um nukleare Formladungen handeln, die ihre Energie überwiegend gebündelt in Richtung der Prallplatte entladen. Dann wird [math]f \approx 1[/math] und der spezifische Impuls

[math]!I_\mathrm{sp} = \sqrt{\frac{8 W_\mathrm{B}}{m_\mathrm{P}}} \, \times \, \frac{1}{g}[/math]

Wie groß ist die Energiedichte von Kernbomben? Wird eine Masse an Plutonium 239 komplett gespalten, werden 80.000 Gigajoule pro kg frei – ca. 19 kt TNT-Äquivalent (1 Tonne TNT-Äquivalent entspricht 4.2 Gigajoule). Fusionsbrennstroffe, die in thermonuklearen Bomben und Fusionsreaktoren zum Einsatz kommen, weisen noch höhere Energiedichten auf: 340.000 Gigajoule (= 80 kt TNT) pro kg bei Fusion von Deuterium mit Tritium, 96.000 Gigajoule (= 23 kt TNT) pro kg bei Fusion von reinem Deuterium.

In nach dem Teller-Ulam-Design aufgebauten Fusionsbomben – und dem Blanket geplanter Fusionskraftwerke – wird das mit dem Deuterium reagierende Tritium durch Neutronenbestrahlung aus Lithium erbrütet (die Bomben enthalten als Fusionssprengstoff Lithiumdeuterit). Bezogen auf die Ausgangskerne Lithium und Deuterium ergibt sich eine Energiedichte von 212.000 Gigajoule (= 50 kt TNT) pro kg.

Natürlich wird in realen Bomben der Kernsprengstoff nicht komplett zur Reaktion gebracht, und der chemische Kompressionszünder, die Elektronik, die Bombenhülle usw. tragen viel zur Gesamtmasse bei. Sehr kleine Spaltungsbomben wie die Granate Davy Crockett haben Energiedichten zwischen 2 und 200 Gigajoule pro kg Gesamtmasse. Größere Bomben liegen bei 100 Gigajoule pro kg, moderne Fusionssprengköpfe erreichen 4600 Gigajoule pro kg.

Für Energiedichten, die größenordnungsmäßig im Bereich zwischen 1 und 1000 Gigajoule pro kg liegen, liefert unsere obige Formel spezifische Impulse zwischen 9000 und 280.000 Sekunden.

Natürlich haben wir bei unseren Abschätzungen viele Vereinfachungen gemacht. In der Praxis sind vermutlich für Spaltungsbomben spezifischen Impulse zwischen 2500 und 10.000 Sekunden machbar, Fusionsbomben könnten bis zu 100.000 Sekunden ermöglichen.

Welcher Schub lässt sich auf diese Weise erreichen? Er berechnet sich aus der Formel

[math]!F = I_\mathrm{sp} \times \dot{M} \times g[/math]

Für [math]\dot{M}[/math] ist hier einfach die Masse der pro Zeiteinheit ausgeworfenen Bomben einzusetzen. Angestrebt wird eine Frequenz von einer Explosion pro Sekunde. Wir wollen Ladungen von je 1 kt Sprengkraft und einer Energiedichte von 30 Gigajoule pro kg (d.h. 140 kg Masse) einsetzen. Damit erhalten wir:

[math]!I_\mathrm{sp} \approx 5 \times 10^4 \, \mathrm{s}[/math]

bzw. unter der konservativen Annahme dass sich 10% hiervon in der Praxis nutzen lassen

[math]!I_\mathrm{sp \, eff} = 5000 \, \mathrm{s}[/math]

sowie für die Kraft

[math]!F = I_\mathrm{sp \, eff} \times \frac{140 \, \mathrm{kg}}{\mathrm{s}} \times g \approx 7 \, \mathrm{MN}[/math]

Dies entspricht ziemlich genau dem Schub eines chemischen F-1-Triebwerks der ersten Stufe der Saturn V oder der Gewichtskraft von 700 t im Erdschwerefeld.

Wir wollen 3000 Bomben „tanken“ (Gesamtmasse 420 t) und 100 t Nutzlast laden. Die Gesamtmasse der Rakete sei 600 t (man beachte, dass wir immer noch zumindest prinzipiell in der Lage sind, Bodenstarts von der Erde durchzuführen!).

Dann ist das Massenverhältnis:

[math]!R = \frac{600}{180} \approx 3.3[/math]

Es ergibt sich eine maximal mögliche Geschwindigkeitsänderung von

[math]!\Delta v = g \, \times \, 5000 \, \mathrm{s} \, \times \, \ln{R} = 5.9 \times 10^4 \, \mathrm{m}/\mathrm{s}[/math]

In Worten: beinahe 60 Kilometer pro Sekunde!

Das ist mehr als für einen Flug von der Erdoberfläche bis zur Marsoberfläche und wieder zurück nötig ist (ca. 50 km pro Sekunde)!

Wir wollen das Konzept noch etwas ausbauen und annehmen, dass wir einen spezifischen Impuls von 50.000 Sekunden nutzen können und Wasserstoffbomben einsetzen, die eine Sprengkraft von 250 kt bei einer Energiedichte von 1000 Gigajoule pro kg (jede 1050 kg) aufweisen.

Damit erhalten wir

[math]!F = 5 \times 10^4 \, \mathrm{s} \times \frac{1050 \, \mathrm{kg}}{\mathrm{s}} \times g \approx 515 \, \mathrm{MN}[/math]

entsprechend der Gewichtskraft von 52.500 Tonnen im Erdschwerefeld.

Wir laden 10.000 Bomben ein (Gesamtmasse 10.500 t) und nehmen 5000 t Nutzlast auf. Die Gesamtmasse der betankten Rakete sei 20.000 t.

Dann ist

[math]!R=\frac{20.000}{9500} \approx 2.1[/math]

und

[math]!\Delta v = 5 \times 10^4 \, \mathrm{s} \times g \times \ln{R} \approx 365 \, \mathrm{km}/\mathrm{s}[/math]

Damit lässt sich vom Erdboden aus fast jeder Körper in unserem Sonnensystem erreichen und auch wieder zurückfliegen – mit einer Nutzlast von 5000 t, entsprechend 11 mal der ISS!

Wir sehen, dass wir hier das Reich der anämischen chemischen Raketen weit hinter uns gelassen haben. Wir sehen keine vielstufigen Treibstofftürme aus Aluminium mit winziger Nutzlast obendrauf (von der nur ein Bruchteil zurückkehrt). Wir sehen ein wuchtiges, bauchiges Gefährt von der Größe eines Wolkenkratzers vor uns, das in einer Marinewerft aus U-Boot-Stahl gefertigt wird, und das Hunderte von Menschen und viele Tausend Tonnen Material zum Mond, zum Mars oder zu den Saturnmonden transportieren kann, und gegebenenfalls auch wieder zurück.

Und dies alles beruht auf heutzutage verfügbaren Technologien. Spaltungs- und Fusionsbomben – auch nukleare Formladungen – sind längst vorhanden. Zur Konstruktion von Prallplatten und Stoßdämpfern sind keine großen technologischen Durchbrüche nötig. Wir haben die Mittel, um das Sonnensystem zu kolonisieren und zu industrialisieren in der Hand!

Das Problem ist hier wiedermal die Politik. Kernbomben wurden bisher nur als Mittel zum Kampf und zur Zerstörung angesehen – sie als neuartigen Treibstoff zu nutzen erscheint vielen auf den ersten Blick wie ein bizarrer Einfall. In den Wirren des Kalten Krieges verbot man im Rahmen des Test Ban Treaty Kernexplosionen in der Atmosphäre und im Weltall. So kam es, dass das Projekt Orion bisher nicht über theoretische Berechnungen und Modellexperimente mit chemischen Sprengladungen hinauskam. Inzwischen hat man wieder angefangen, behutsam darüber nachzudenken. Dabei spricht man meist von „Pulsed Plasma Propulsion“ und vermeidet das Reizwort „Atombombe“.

Gesetze lassen sich – mit Ausnahme der physikalischen – ändern. Wann wird die Menschheit so vernünftig, dass sie Schwerter zu Pflugscharen umschmiedet und ihre Vorräte an waffenfähigem Material und Expertise im Bau von Kernsprengladungen nutzt, um das Sonnensystem friedlich zu erschließen?

Dokumentation

• Michael Flora: Project Orion: Its Life, Death, and Possible Rebirth – Geschichte des Orion-Projekts.
• Freeman Dyson (1968): Interstellar Transport – Dyson stellt das Projekt, an dem er selbst mitgearbeitet hat, vor, schätzt die Leistungsfähigkeit des Antriebskonzeptes ab und extrapoliert es bis zu interstellaren Missionen der Zukunft.
• J. C. Nance (1965): Nuclear Pulse Propulsion – technische Übersicht.
• Bonometti et al. (2000): External Pulsed Plasma Propulsion and its Potential for the Near Future – Das Orion-Projekt unter aktuellen Gesichtspunkten.
• Final Frontier: Die Rückkehr des Orion-Projektes – Matthias Meier stellt eine interessante Analogie her zwischen dem politisch bedingten Ende der Segelschiffs-Expeditionen Chinas im Mittelalter und der noch nicht erfolgten Realisierung von Orion in unserer Zeit.
• Video: Project Orion: A Re-Imagining – in dem kurzen computeranimierten Film startet das Raumschiff zunächst mit einem Cluster von Feststoffboostern und schaltet oberhalb der Atmosphäre den nuklearen Pulsantrieb ein.

Man kann sich die Frage stellen, ob sich nicht auch eine stetig arbeitende Variante des Orion-Antriebes konstruieren lässt – ein Triebwerk mit ähnlichen Leistungswerten, aber konstantem Schub anstatt explosiver Dampfhammerschläge, die mit einem Stoßdämpfermechanismus abgefedert werden müssen?

Robert Zubrin entwarf eine derartige Maschine. Die nukleare Salzwasserrakete hat das Ziel, eine konstant brennende prompt-überkritische Kerndetonation aufrechtzuerhalten. Dies geschieht, indem Wasser, in dem ein Uran- oder Plutoniumsalz gelöst ist, aus schmalen Röhren, die mit Neutronenabsorbern umgeben sind, in eine Brennkammer geleitet wird, die mit Neutronenreflektoren umgeben ist: Dort wird die Lösung prompt-überkritisch, und es entsteht eine konstante Reaktionszone, in der die Lösung zu Plasma explodiert, das mit hoher Geschwindigkeit aus einer Düse strömt.

Dieser Entwurf ist, im Gegensatz zu Orion, noch sehr theoretisch. Robert Zubrin zufolge lässt sich, indem die Reaktionszone von reinem Wasser umströmt wird, die Energie schnell genug abtransportieren, dass die Brennkammerwände nicht verdampfen. Wird sich diese Technologie praktisch umsetzen lassen? Zukünftige Experimente werden es zeigen müssen!

Dokumentation

• Robert Zubrin (1991): Nuclear Salt Water Rockets: High Thrust at 10.000 Sec Isp
• John Cramer: Nuke Your Way to the Stars (populärwissenschaftlicher Bericht)

Ob Orion-Raketen – oder nukleare Salzwasserraketen – vom Erdboden aus starten dürfen, ist debattierbar. Sie haben natürlich den „Pferdefuß“, dass sie größere Mengen an Radionukliden ausstoßen. Es gibt jedoch Berechnungen, nach denen die von Orion-Starts freigesetzte Radioaktivität, wenn sie von einer Plattform mitten im Pazifik aus erfolgen würden, im natürlichen Strahlungshintergrund unterginge.

Ansonsten muss der Transport von der Erdoberfläche ins LEO mit anderen Mitteln erfolgen: Große chemische oder nuklear-thermische Raketen, Weltraumflugzeuge a la Skylon, Laser- oder Mikrowellen-Startrampen, Magnetkatapulte, Lofstrom-Schlaufen oder in der Zukunft auch Orbitalaufzüge.

Viele sehen den Kernfusions- oder auch Antimaterieantrieb als Fernziel der Raketentechnik an. Beide sind sehr hypothetisch. Antimaterie kann heute erst in mikroskopischen Mengen unter sehr hohem Energieaufwand in Beschleunigern hergestellt werden. Konstant brennende, nichtexplosive Kernfusion wurde noch nicht unter Energiegewinn realisiert – dies könnte sich allerdings im Zuge des ITER-Projekts bald ändern. Jedoch sind Magneteinschlussmaschinen (Tokamak und Stellarator), wie man sie zur Energiegewinnung auf der Erde nutzen möchte, für Raumschiffantriebe vermutlich zu massereich pro erzeugter Schubkraft. Eventuell könnte ein Fusionsverfahren, das man früher als vielversprechendes Konzept zur Stromerzeugung ansah, heute aber in diesem Zusammenhang eher skeptisch betrachtet, sich als günstig zum Antrieb von Raumschiffen erweisen: Der Trägheitseinschluss. Bei diesem werden Brennstoffpellets durch allseitige Laserbestrahlung sehr stark erhitzt und vom Rückstoß des verdampfenden Materials komprimiert, wodurch die Fusion gezündet wird. Die Studien Daedalus und Icarus der British Interplanetary Society, deren Ziel es ist, ein unbemanntes Raumschiff zu entwerfen, das mit 200 t Nutzlast innerhalb von 100 Jahren zu einem Exoplanetensystem fliegt, fassen diese Antriebsmethode ins Auge. Die Pellets werden dabei in einer halbkugelförmigen Triebwerksschale gezündet und das Plasma von Magnetfelder gebündelt nach hinten ausgestoßen.

Ein besonders visionäres Konzept entwickelte Robert Bussard: Wozu Treibstoff mitnehmen, wenn man ihn unterwegs einsammeln kann? Der Bussard Ramjet saugt das äußerst dünne, interstellare Wasserstoffgas mit einem riesigen Trompetentrichter (Hunderte km Durchmesser) und einem noch riesigeren von diesem erzeugten Magnetfeld (Tausende km Durchmesser) an und nutzt es als Fusionsbrennstoff. Theoretisch wäre es mit einem solchen Schiff möglich, konstant mit einem g beliebig lange zu beschleunigen: Dank relativistischer Zeitkontraktion wären hierdurch innerhalb eines Menschenlebens alle Himmelskörper im beobachtbaren Universum erreichbar!

Dies ist jedoch ein äußerst futuristisches Konzept, das im 21. Jahrhundert vermutlich noch nicht realisiert werden wird. Etwas naheliegender ist ein anderer Entwurf von Bussard, der darauf beruht, dass mit einem sogenannten Fusor – einem Fusionsreaktor, der auf elektrostatischem Einschluss beruht und im Vergleich mit Magneteinschlussmaschinen sehr leicht ist – erzeugte Energie zum Antrieb von relativistischen Elektronenbeschleunigern dienen soll, deren Partikelstrahlen wiederum das Arbeitsgas des Raketenantriebs erhitzen: Bussard et al. (1995): Inertial-Electrostatic-Fusion Propulsion Spectrum: Air-Breathing to Interstellar Flight.

Kontrollierte, stetig brennenden Fusion ist eine Energiequelle der Zukunft. Heutzutage können wir jedoch schon mithilfe von Kernspaltung oder auch explosiver Fusion sehr leistungsstarke Raketenantriebe bauen, mit denen wir das Sonnensystem erschließen können. Wann hören wir auf, uns um irdische Ölquellen zu streiten und brechen mithilfe der Supernova-Treibstoffe in den Kosmos auf?

Weitere interessante Webseiten zu diesem Themenbereich

• J. C. Newby: The History and Mathematics of Rockets
• News: Plutonium to Pluto – Russland plant, eine nuklear-elektrisch angetriebene Raumsonde zu entwickeln (ein Kernreaktor treibt einen Ionenantrieb).
• 100 year Starship Initiative – können wir in 100 Jahren ein Raumschiff bauen, das uns zu einem Exoplanetensystem bringt?
• Project Rho: Atomic Rockets – eine herausragende, umfassende Webseite von Winchell Chung über Raumfahrt und Raketen. Sie ist primär als Informationsquelle für Science-Fiction-Autoren gedacht, die ihre Geschichten fest in der physikalischen Realität verankern und sich an das halten wollen, was im Rahmen wirklich konstruierbarer Raumschiffantriebe möglich ist. Die Seite kann aber jedem, der sich für Raumfahrt und nukleare Raketenantriebe interessiert, uneingeschränkt empfohlen werden!